第九届线上物理竞赛试题和参考答案发布
发布时间:2023-11-27 09:30:00
OPhO官网终于上线啦!
每届OPhO结束后,我们都会公开发布该届的试题和参考答案。由于解析属于OPhO参与奖的一部分,因此我们公开发布的内容中不含解析。
我们首先发布第九届OPhO的试题和参考答案,供大家参考。您可以点击下方按钮下载pdf格式的试题和参考答案文件,也可以直接在本网页上阅读试题和参考答案。我们之后会陆续发布更早的OPhO的试题和参考答案,敬请关注!
特别提醒:此处pdf文件版的第九届线上物理竞赛预赛试题、第九届线上物理竞赛预赛参考答案、第九届线上物理竞赛决赛试题、第九届线上物理竞赛决赛参考答案均使用署名-非商业性使用-禁止演绎4.0国际许可协议进行许可,请务必遵守此协议!
第九届OPhO预赛试题
单选题:在每道题的4个选项中,有且仅有1个选项是符合题意的,第1-10题每题5分,第11-20题每题10分
- 在一定气压下,任何晶体的熔点与其相应液体的______相同.
- 沸点
- 闪点
- 凝固点
- 自燃点
- 以下四种电磁波中频率最高的是______.
- X射线
- 可见光
- 紫外线
- 无线电波
- 一张纸厚度的数量级为______.
- $10^{-1}\mathrm{m}$
- $10^{-2}\mathrm{m}$
- $10^{-3}\mathrm{m}$
- $10^{-4}\mathrm{m}$
- 一个体积为 $V$ 的容器内有 $N$ 个气体分子,则气体分子间的平均距离大致是______.
- ${V}^{\frac{1}{3}}$
- $\frac{{V}^{\frac{1}{3}}}{N}$
- $\left(\frac{V}{N}\right)^{\frac{1}{3}}$
- $\frac{1}{N}\left(\frac{V}{N}\right)^{\frac{1}{3}}$
- 自然光在经大气中小水滴的折射及反射后形成的光谱称为彩虹,关于彩虹,下列叙述不正确的是______.
- 彩虹现象可以解释为不同波长的光在水滴中的折射率不同从而引起了光的色散
- 完整的彩虹是圆形的,只是观察者通常在地面附近因此只能看到彩虹一部分
- 可能同时有多道彩虹的出现,这些彩虹通常是光线在水滴中经过多次的反射形成的
- 太阳和彩虹通常位于观察者的同一侧
- 某辆车在以速率 $v$ 做匀速直线行驶中,看见正前方有一座山,车主在鸣了一次笛后过了 $t$ 时间听见回声,若声速记为 $c (v < c)$ ,则该车主听见回声的时刻,车到山的距离大致是______.
- $\frac{c+v}{2}t$
- $\frac{c-v}{2}t$
- $\frac{c-2v}{2}t$
- $\frac{2c-v}{2}t$
- 一辆停在高空的升降电梯中站有一个质量为 $m$ 的人,某时刻起,电梯开始缓慢下降,一段时间后到达地面平稳停下,电梯下降高度为 $h (h > 0)$ ,人相对于电梯始终静止不动,只考虑人受到的重力和电梯对人的支持力. 重力加速度大小为 $g$ ,则整个过程电梯对人做功为______.
- $0$
- $mgh$
- $-mgh$
- 条件不足
- 直流电在现代医疗中有着丰富的应用,下列叙述正确的是______.
- 给人体施加电压会在体内产生电场从而出现直流电,这会引起细胞中的异号离子在细胞膜的两侧聚集,改变膜的通透性. 细胞膜两侧的离子产生的附加电场在细胞内部与外电场反向
- 电解质溶液中的微粒在外加电场下的迁移称作电泳,电泳可以分离血浆中的不同蛋白. 即使是溶液中的电中性的微粒,也同样会在外加电场下定向迁移
- 直流电会在人体内产生电解作用,体液中含有大量Na$^+$和Cl$^-$离子,当通以直流电时,Na$^+$和Cl$^-$分别向阳极和阴极移动,并在电极上电中和
- 病毒或生物大分子一般携带负电荷,这是因为它们相比其它微粒更容易获得电子,这种带电过程属于感应起电
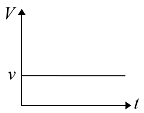
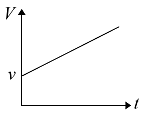
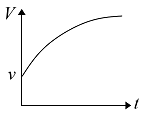
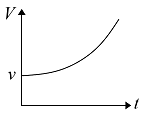
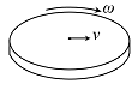
- 如图所示,地面上放置着一个以恒定的角速度转动的圆盘,圆盘的中心固定不动. 圆盘中心站着一个人,若此人以恒定的速率 $v$ (按照他自己的视角看来,圆盘静止不动,自己的速率始终为 $v$ )从圆盘中心沿半径走到圆盘的边缘,则以站在圆盘外的人看,这个行走的人的速率 $V$ 随着时间 $t$ 变化的大致关系是______.
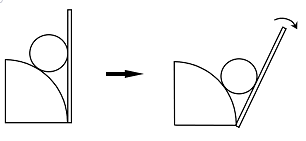
- 如图所示,地面上有一个固定的1/4圆柱,在圆柱的右侧有一个挡板起初竖直放置并与圆柱相切,在圆柱和挡板之间放一个半径不超过圆柱半径的刚性球,现以挡板的下边缘为轴,开始缓慢顺时针转动挡板,直到挡板被转至水平,球与圆柱、挡板之间没有摩擦力,则在转动挡板的过程中,挡板对球的作用力的变化是______.
- 增大
- 减小
- 先减小后增大
- 条件不足
- 古希腊的 Eratosthenes 首次估算了地球半径, Aritarchus 随后成功估算了月球半径、太阳半径、月地距离和日地距离,以下估算结果明显不正确的是______.
- 利用月食估算月地距离,若初亏时刻为 $T_1$ ,食既时刻为 $T_2$ ,复圆时刻为 $T_3$ ,地球半径是 $r_e$ ,则月球半径约是 $(T_2-T_1)r_e/(T_3-T_2)$
- 使用一个半径为 $r_c$ 的硬币,用一只眼睛观察硬币,当硬币恰好遮盖住月亮时硬币到眼睛的距离为 $d$ ,若月球半径是 $r_m$ ,则月地距离约是 $r_md/r_c$
- 当月亮刚好是半月时,若在地面上一点看向太阳和看向月亮之间的视线夹角为 $\theta$ ,若月地距离是 $L_m$ ,则日地距离约是 $L_m/\sin\theta$
- 利用日食估算太阳半径,由于在日食的食甚时刻,月亮几乎刚好遮蔽住太阳,因此若月球半径是 $r_m$ ,月地距离是 $L_m$ ,日地距离是 $L_s$ ,则太阳半径约是 $r_mL_s/L_m$
- 一个点电荷系统的电偶极矩的定义是 $\vec{p}=\sum q\vec{r}$ ,也就是对所有点电荷的电荷量和其位置矢量的乘积求和. 类似于电偶极矩,我们可以定义“质量偶极矩”. 系统电偶极矩随时间的变化率不为常数时会辐射电磁波,这就是电偶极辐射. 然而,在引力波辐射中却并不存在“质量偶极辐射”,究其原因是______.
- 质量守恒
- 动量守恒
- 电荷量有正负之分,但现实中却没有负质量物体
- 变化的电场产生磁场,变化的引力场却没有“磁场”的对应物
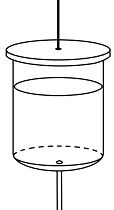
- 有一种沙画,艺术家使用一个悬吊的容器装满沙子,并通过控制沙子的落下来创作绘画. 如图所示就是一种作沙画的容器,该容器可近似看作是个底面积为 $A$ ,高度为 $H$ 的圆柱,圆柱底面正中心有开有一个小孔,容器内的沙子能够均匀地垂直落下,用一根轻质悬绳系在圆柱顶面中心使容器吊在空中. 若现在容器内装满密度为 $\rho$ 的沙子,底面小孔单位时间内流出沙子的质量恒为 $m$ ,容器从开始到漏完沙子始终保持静止,空容器的质量为 $M$ ,重力加速度大小为 $g$ ,则容器漏沙子的整个过程顶部悬绳的平均张力为______.
- $Mg+\frac{\rho AHg}{2}-\frac{m^2}{\rho A}$
- $Mg+\frac{\rho AHg}{2}-\frac{m^2}{\rho H^2}$
- $Mg+\frac{\rho AHg}{2}-\frac{m^2}{2\rho A}$
- $Mg+\frac{\rho AHg}{2}-\frac{m^2}{2\rho H^2}$
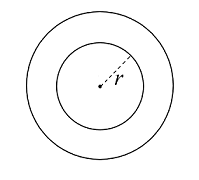
- 如图所示,将一个半径为 $r$ 的发光球面浸在一个折射率为 $n$ 的球形介质内,使介质球和发光球面共球心,发光球面的内部也填满了该种介质,光线可以穿过发光球表面,介质外部的折射率可视为 $1$ . 通过调整介质球半径,可能使得发光球在经过介质的表面折射后在介质外部形成一个球面虚像,则该虚像的半径为______.
- $nr$
- $ n^2r$
- $\frac{n+1}{n}r$
- $\frac{n}{n-1}r$
- 如图所示,现有一足够长的倾角为 $\theta$ 的固定斜面和一质地均匀、厚度一致的薄毯,薄毯的长度为 $L$ . 现将薄毯沿长度方向紧密地卷成圆柱. 将卷好的薄毯按图所示在斜面上由静止释放,薄毯在重力作用下逐渐下滚铺开. 若斜面足够粗糙,使得已铺开的部分不会在斜面上滑动,重力加速度大小为 $g$ ,则薄毯由静止到完全铺开的用时为______.
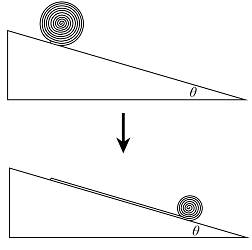
- $\sqrt{\frac{3L}{2g\sin\theta}}$
- $\sqrt{\frac{3L}{g\sin\theta}}$
- $\sqrt{\frac{2L}{3g\sin\theta}}$
- $\sqrt{\frac{6L}{g\sin\theta}}$
- 使用光束照射物体可能促使物体内部电子逸出形成光电流,这就是光电效应. 关于光电效应,下列叙述不正确的是
- 发生光电效应时,光电子在照射光的入射方向上从物体中发射出来的概率大于其它方向
- 光电子射出物体时的最大动能可以用 $E_k=h\nu-W$ 来计算,其中 $\nu$ 是光子能量, $W$ 是材料的逸出功, $h$ 是普朗克常数
- 如果将光电效应视为某种微观过程,则其逆过程是电子与静止离子复合为原子并辐射出光子的“辐射复合”
- 在照射光的频率增大达到一定大小时,光电流趋于饱和,这时候继续增大光电流,光电流有可能下降,光电流发生显著下降时的频率称为光电效应的“蓝限”
- 如图所示,四根平行的电阻不计的光滑无限长直导轨倾斜放置,互相之间等距. 在导轨一端,每两根导轨之间各接一电路元件,分别是初始不带电的电容 $C$ 、定值电阻 $R$ 、不计内阻且电动势恒定的直流电源 $E$ . 在导轨上横置一个有电阻的均质金属棒,金属棒与四条导轨均接触良好,金属棒初始与导轨最上方的MN平行,空间中有竖直向下的匀强磁场,金属棒与导轨的最上方之间有四个断开的开关. 现将金属棒无初速度地从导轨上释放,使其在重力作用下沿导轨下滑. 若某人在之后先后闭合四个开关中的三个,若金属棒在闭合开关前后始终保持与MN平行,则此人依次闭合的三个开关只可能分别是______.
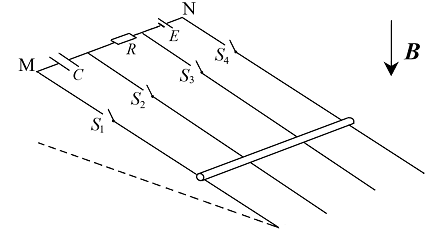
- $S_1, S_3, S_2$ 或 $S_3, S_1, S_2$
- $S_1, S_4, S_2$ 或 $S_4, S_1, S_2$
- $S_1, S_4, S_3$ 或 $ S_4, S_3, S_1$
- $S_2, S_3, S_4$ 或 $S_3, S_2, S_4$
- 如图所示,两根不可伸长的轻质悬线的一端同时固于O点,长度均为 $l$ ,另一端分别各接一带相等电量正电的质量相同的点电荷. 在平衡时,两条悬线与竖直方向的夹角均为 $\theta$ . 现同时给两个点电荷施加水平的初速度,方向相反. 若后续运动过程中两根悬线偏离平衡位置的夹角始终很小,重力加速度大小为 $g$ ,不计一切损耗,则该振动系统的周期为______.
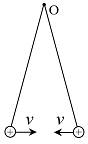
- $2\pi\sqrt{\frac{l\cos\theta}{g(1+2\cos^2\theta)}}$
- $2\pi\sqrt{\frac{l\cos\theta}{g(1+2\cos\theta)}}$
- $2\pi\sqrt{\frac{3l\cos\theta}{g(1+2\cos^2\theta)}}$
- $2\pi\sqrt{\frac{3l\cos\theta}{g(1+2\cos\theta)}}$
- 考虑两个体积恒定的绝热容器,里面充入密度和温度完全相同的理想气体,其中一个容器远大于另一个,大的容器所含气体的量可以视为无穷. 现给小的容器内的气体加热,使其吸收热量 $Q$ 后温度升高到原来的 $k$ 倍,然后使用一卡诺热机分别以小容器和大容器作为高低温热源对外做功. 已知理想气体的内能正比于温度,则该卡诺热机可以输出的最大功为______.
- $\frac{\ln (k+1)}{\ln (k+1)+1}Q$
- $\frac{\ln k}{\ln (k+1)+1}Q$
- $ \left(1-\frac{\ln k}{k-1}\right)Q$
- $\left(1-\frac{\ln k}{k+1}\right)Q$
- 在地面附近以大小为 $v_0$ ,方向与重力方向的夹角为 $\theta$ 的初速度向空中抛出一个质量为 $m$ 的质点. 假设该质点只受重力和空气阻力的作用,重力的大小和方向均恒定,重力加速度大小为 $g$ ,空气阻力的大小始终近似为质点速率的 $k$ 倍,方向始终与质点的速度相反. 仅考察质点在空中运动的过程,则下列说法正确的是______.
- 质点运动的最大速率只可能约为 $v_0$ 或 $\frac{mg}{k}$
- 质点运动的最小速率只可能约为 $v_0$ 或 $\frac{mgv_0\sin\theta}{\sqrt{k^2v_0^2+{m^2g^2}-2v_0{mgk}\cos\theta}}$
- 质点竖直方向的最大位移大小只可能约为 $\frac{mv_0\sin\theta}{k}$
- 质点竖直方向的最大位移大小只可能约为 $\frac{m}{k}\sqrt{v_0^2+\frac{m^2 g^2}{k^2}-2 v_0 \frac{m g}{k} \cos \theta}$
第九届OPhO预赛参考答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | A | D | C | D | B | C | A | D | D | C | B | A | B | B | A | D | A | C | B |
第九届OPhO决赛试题
解答题:从下列四道选题中任选两道作答,每道题75分,多做的部分不给分
- 时间旅行作为一个广受欢迎的科幻概念,在过去数十年不断吸引万千文学⼯作者们创作相关作品。然而对于物理学⼯作者,时间旅行并非一个幻想,甚至是⼀个能够经得起严谨数学推敲的有趣问题. 对时间旅行能提出至少两个问题:(1)现代物理学理论框架中是否存在时间旅行的可能性及实验设想,(2)若能够进行时间旅行, 我们能从基本物理原理出发对其作出何种预言. 在本题中我们关注第二个方面,来对时间旅行的衍生效应进行一定的理论研究. 这类研究曾在1991年由Thorne和Deutsch分别在经典力学和量子力学的视角下讨论,本题中初等地来分析理解其中的思想,不计相对论效应. Thorne等人对时间旅行问题作出的最核心的要求即自洽性:即时间旅行不应当引起任何因果律的破坏. 一个著名例子即祖父悖论:时间旅行者回到过去杀死年轻时自己的祖父. 由于按照通常的时间进程时间旅⾏者不会出生,因此祖父的死也将无从谈起. 在Thorne等人的要求下,祖父悖论可以被解释为过程中会发生各种和时间旅行者的记忆一致的事件来保护祖父不被杀死.
- 写出动量守恒定律的内容. (3分)
- 考虑一个二维平面 $Oxy$ ,时刻 $t=0$ ,一质点通过坐标 $(-x,0)$ 以恒定速率 $v$ 沿 $Ox$ 正方向运动. 在坐标 $(0,x)$ 处存在一个时间旅行器,它将任何进入通过此点的质点传送回到 $\tau$ 时间前的坐标 $(0,-x)$ ,并将其速度改变为沿 $Oy$ 正方向,大小相等的值. $\tau,x$ 为已知量,给出不引起祖父悖论的 $v$ 的取值范围. (6分)
- 考虑 $Oxy$ 平面内向量的转动,已知初始向量为 $\vec{x}$ ,转动角度为 $\theta$ ( $\theta$ 为正代表迎着 $Oz$ 轴看转动为逆时针),这样的转动也被用向量 $\vec{\theta}=\theta \vec{k}$ 代表. 试用 $\vec{x}$ 及 $Oz$ 轴单位向量 $\vec{k}$ 表示转动后的向量. (6分)
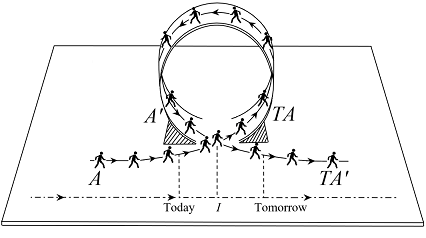
- 可以看到,时间旅行问题中最简单的抽象有着如下的图像,如图所示,考虑研究对象 $A$ ,经历时间旅行影响自己(带箭头的实线代表 $A$ 的时间流动), 在旁观者(时间正确流动,由图中下方点横线代表)的视角下, 某时刻出现了来自未来的对象 $A^\prime$ ,其与 $A$ 在时刻 $I$ 发生通常的相互作用后得到对象 $TA,TA^\prime$ . 符号 $T$ 代表经历相互作用. 自洽条件要求:\[TA=A^\prime\]而 $TA^\prime$ 即为整个作用过程下,研究对象 $A$ 最后的末态.
 考虑两质量相同的质点的弹性碰撞过程,设入射动量和出射动量在同一平面内,动量分别为 $\vec{p}_1, \vec{p}_2$ . 已知质心系中物体1的动量方向转动为 $\vec{\theta}=\theta\vec{n}$ . 试求碰撞后两物体的动量. (14分)
考虑两质量相同的质点的弹性碰撞过程,设入射动量和出射动量在同一平面内,动量分别为 $\vec{p}_1, \vec{p}_2$ . 已知质心系中物体1的动量方向转动为 $\vec{\theta}=\theta\vec{n}$ . 试求碰撞后两物体的动量. (14分) - 映射 $T$ 描述的正是像(4)中这样的动量变化,简单起见我们可以描述为 $\vec{p}^\prime_i=T\vec{p}_i$ ,其中 $i=1,2$ . 如果(4)中的物体2是碰撞后通过时间旅行器回到过去的物体1(假设通过时间旅行器动量保持不变),只考虑一次碰撞,试求物体1最终动量. (20分)
- 考虑平面 $Oxy$ , $t=0$ 时一质点通过坐标 $(-x,0)$ 以速率 $v$ 沿 $Ox$ 正向运动. 在平面上某处存在一个时间旅行器,它将任何进入通过此点的质点传送回到 $\tau$ 时间前的坐标 $(0,-x)$ ,并将其速度改变为沿 $Oy$ 正方向,大小相等的值. 若质点通过时间旅行器回到过去并和过去的自己以平方反比斥力 $\vec{F}=\alpha \vec{{r}}/r^3$ 相互作用, $\alpha$ 为已知常数. 若质点回到过去的时刻恰是 $t=0$ 且速率同样是 $v$ ,而 $v,x$ 已知,试求满足自洽条件的 $\tau$ 、时间旅行器的坐标及质点最终的速度. (26分)
- 物质的微观结构一直是物理学家感兴趣的问题,了解物质的基本粒子组成可以帮助我们更加深刻地认识世界、理解更多基本物理规律。历史上曾有人提出过一种弱子模型,并借助这种模型理解温度、熵这些热力学概念,该模型尚未被实验验证. 弱子模型认为,轻子、夸克、光子等人们熟知的粒子均是由 $6$ 种弱子: $\nu_e$ 、 $\nu_\mu$ 、 $\nu_\tau$ 、 $\omega^\star$ 、 $\omega_1$ 、 $\omega_2$ 及其反粒子构成的,表示反粒子的符号上加一条横线,如 $\nu_e$ 对应的反粒子是 $\bar{\nu}_e$ ,粒子与其反粒子的固有质量相同、电荷量大小相等但电性相反,弱子均为自旋为 $1/{2}$ 的费米子,每个弱子都带 $1$ 个单位的弱荷 $g_w$ ,弱荷是产生弱相互作用的原因.
- 简要说明基本粒子的弱子模型目前还未被实验验证的原因,猜测实验上可能存在怎样的困难. (4分)
- 已知当弱子不发生衰变也不发生散射时,其能量将保持恒定,以光速运动的弱子固有质量为0,试在此情景下根据相对论中能量和动量的关系定性阐述弱子获得固有质量的机制. (6分)
- 字母 $\nu$ 表示的三种弱子属于三种中微子,这是一类不带电的粒子,另外质子 $p$ 、中子 $n$ 、电子 $e^-$ 所带的电荷量分别为 $+1e$ 、 $0e$ 、 $-1e$ ,其中 $e$ 是元电荷. 假设质子 $p$ 和中子 $n$ 的夸克组成分别为:\[p=uud\quad\qquad n=udd\]上夸克$u$、下夸克$d$和电子$e^-$的弱子组成分别为:\[u=\omega^\star\omega_1\bar{\omega}_1\qquad d=\omega^\star\omega_1\omega_2\qquad e^-=\nu_e\omega_1\omega_2\]试利用上述信息求出弱子$\omega^\star$所带的电荷量. (8分)
- 光子 $\gamma$ 是一种不带电的玻色子,其弱子组成是:\[\gamma=\cos\theta_\omega\omega_1\bar{\omega}_1+\sin\theta_\omega\omega_2\bar{\omega}_1\]其中 $\theta_\omega$ 是描述两种组合方式所占比例的一个参数,例如组合 $\omega_1\bar{\omega}_1$ 所占比例为其系数的平方 $\cos^2\theta_\omega$ ,对于某个特定的光子而言,其弱子构成仅可能是两种组合方式中的一种. 在(2)的条件下,试简要分析为什么电子不可能由 $2$ 个弱子构成,而光子则可能. (11分)
- 弱荷为 $g_1$ 、 $g_2$ 的粒子之间的弱相互作用势关于粒子之间的距离 $r$ 的表达式为:\[\varphi(r)=Kg_1g_2\left(\frac{\mathrm{e}^{-kr}}{r}-\frac{B\left(1+2kr\right)\mathrm{e}^{-2kr}}{\rho}\right),\]其中 $K$ 、 $k$ 、 $B$ 、 $\rho$ 均为大于 $0$ 的已知常数,它们仅与参与弱相互作用的两个粒子的种类相关. 试求单个电子与单个光子之间的弱相互作用力关于它们之间的距离 $r$ 的表达式,并据此定性解释电子轫致辐射(即电子做变速运动时将辐射电磁波)的现象和电子吸收光子的现象分别是如何发生的. (13分)
- 考虑处于热力学平衡态的系统,它包含 $N$ 个粒子,这些粒子可占据的能级有 $N_E$ 个,第 $n$ 个能级的能量为 $\varepsilon_n$ ,其中 $n=1,2,\cdots,N_E$ ,第 $n$ 个能级的简并度(即一个能级上允许的量子态数)为 $h_n$ . 假设系统遵循玻尔兹曼分布,即第 $n$ 个能级上的粒子数为:\[a_n=\frac{N}{\sum_n h_n\mathrm{e}^{-\frac{\varepsilon_n}{kT}}}h_n\mathrm{e}^{-\frac{\varepsilon_n}{kT}}\]其中 $k$ 是玻尔兹曼常数, $T$ 是系统的热力学温度. 有人认为,当系统的总能量恒定时,可以将温度的物理意义解释为系统能级上不同的粒子数分布,试跟据以上知识分析此说法的合理性. (13分)
- 由光子构成的气体服从的是玻色分布,假设能量为 $\varepsilon_n$ 的能级的简并度为 $g_n$ (即第 $n$ 个能级上存在 $g_n$ 个可能的光子量子态),每个能级上的光子数为:\[a_n=\frac{g_n}{\mathrm{e}^{-\frac{\varepsilon_n}{kT}}-1}\]已知系统的熵可以通过下式计算:\[S=k\left(\ln Z-\alpha \frac{\partial}{\partial \alpha} \ln Z-\beta \frac{\partial}{\partial \beta} \ln Z\right)\]其中 $Z=\sum_n g_n\mathrm{e}^{-\frac{\varepsilon_n}{kT}}$ . 对光子气体来说 $\alpha=0, \beta=1/kT$ . 若系统满足 $a_n\ll g_n$ ,试推导用 $a_n, \varepsilon_n, k, T$ 这些量表达的光子气体熵. (20分)
- 现有某种均匀的透明的光学介质,折射率为1.5,若光线从空气中入射到该介质的表面时,反射光与折射光的振幅与入射光的振幅之比分别为 $r_1,t_1$ ;此处的反射光的相位会发生突变(半波损失),因此 $r_1 < 0$ . 另一方面,光线从介质内部入射到介质和空气的分界面上,反射光与折射光的振幅之比分别为 $r_2,t_2$ . 忽略该种介质对光的吸收,空气的折射率为1,忽略全反射的可能.
- 简要阐述什么是光的干涉以及光的干涉发生的条件. (5分)
- 已知光的强度及亮度正比于光的振幅的模平方与介质折射率的乘积,若 $r_1=-t_1$ , $r_2=t_2$ . 试求光线垂直入射时 $r_1,t_1,r_2,t_2$ 的值. (5分)
- 在(2)的条件下,用该种介质制作一块足够大的厚度均匀的薄膜,使用一束真空波长等于该薄膜厚度的单色平行光垂直照射在一个无反射的接收屏S上,如图所示,然后再将薄膜在接收屏前与屏平行放置,试求此时屏上的亮度与原先亮度之比. (15分)

- 在(3)的条件下,同样波长的点光源 $p$ 发射的光(不同方向上的光没有恒定相位差)通过一个凸透镜成为平行光,再通过另一个凸透镜汇聚在其焦平面位置的接收屏S上,屏上出现一个光斑 $p^\prime$ ,如下图左图所示. 然后使光通过第一个透镜后射在(3)中的薄膜表面,发生多光束干涉后,再经凸透镜汇聚在焦平面的接收屏S上,如下图右图所示,薄膜与入射光线的夹角为 $\pi/4$ ,为简单起见,假设此时 $r_1,t_1,r_2,t_2$ 的值与垂直入射时相同. 忽略任何介质对光能的吸收,所有凸透镜全同且都足够大. 试求后一种情况下的光斑与前一种情况下的光斑的亮度之比. (20分)

- 在(4)的条件下,分别将两种情况的点光源 $p$ 和第一个凸透镜换为一个单缝 $G$ ,从单缝中发射出的波长与(4)中相同的相干光在如图所示的左图中经过凸透镜并在焦平面位置的接收屏S上出现夫琅禾费衍射条纹,在右图中单缝中发出的相干光在经过(4)中的薄膜的多光束干涉后透过上方的凸透镜,在焦平面位置的接收屏S上出现衍射条纹. 薄膜与单缝缝宽方向的夹角为 $\pi/4$ . 忽略任何介质对光能的吸收,凸透镜全同且都足够大. 在前一种通常的夫琅禾费衍射中,衍射条纹相对于中心线的分布是对称的,但是后一种情况不然. 试求后一种情况下,衍射角(即单缝出射光与垂直于单缝所在平面的直线之间的夹角)分别为 $+\pi/6$ 和 $-\pi/6$ 的光线在屏S上的斑纹的亮度之比. (30分)

- 考察使用电阻丝围成的自相似电阻网络,如图所示,已知三幅图中的所有实线都代表单位长度电阻值完全一致的电阻丝,实线的交汇点代表电阻丝相接的电路节点,图线长度正比于电阻丝长度,且每一幅图的最外层均是正三角形,其单条边的电阻值为 $R$ .

- 最左图的自相似电路构造方法是:使用无穷多条直电阻丝,每条电阻丝的两端接在AB与AC上,并使接点与C构成一个正三角形,尺度是上一级正三角形的一半. 试求A与B间的等效电阻. (5分)
- 在(1)的条件下,试求最左图中A与C间的等效电阻. (12分)
- 在(1)的条件下,若使用一根理想导线接通B与C点,试求此时A与B间的等效电阻. (12分)
- 中间图的自相似电路构造方法是:使用无穷多个电阻丝组成的正三角形相互嵌套在一起,每个正三角形的三个顶点均与其外层的正三角形的三条边的中点分别相接. 试求此时A与B间的等效电阻. (12分)
- 在(4)的条件下,试求A点与从外向内数第 $n(n\rightarrow \infty)$ 个正三角形的任一个顶点间的等效电阻. 若使用一根理想导线接通B与C点,该等效电阻变为多少?(14分)
- 最右图的电路是中间图情形的一种自然推广:仍然使用无穷多个电阻丝组成正三角形相互嵌套,但是每个正三角形的顶点并不接在其外一层正三角形的边的中点上,而是接在黄金分割点上,例如,AD $:$ AC $=(\sqrt{5}-1)/2$ . 试求此时A与B间的等效电阻. (20分)
第九届OPhO决赛参考答案
-
- 动量守恒定律:如果一个系统不受外力,或者外力的矢量和为零,则这个系统的总动量 $\boldsymbol{p}=\sum m\boldsymbol{v}$ 保持不变.
\[v \neq \frac{2x}{\tau}\]- 转动后的向量$\vec{x}^{\prime}$为:\[\vec{x}^{\prime}=\cos \theta \vec{x}+\sin \theta \vec{k} \times \vec{x}\]
\[\begin{aligned}& \vec{p}_1^{\prime}=\frac{\vec{p}_1+\vec{p}_2}{2}+\cos \theta \frac{\vec{p}_1-\vec{p}_2}{2}+\sin \theta \vec{n} \times \frac{\vec{p}_1-\vec{p}_2}{2}, \\& \vec{p}_2^{\prime}=\frac{\vec{p}_1+\vec{p}_2}{2}-\cos \theta \frac{\vec{p}_1-\vec{p}_2}{2}-\sin \theta \vec{n} \times \frac{\vec{p}_1-\vec{p}_2}{2} \end{aligned}\]
\[ \vec{p}_1\]- 时间旅行器横 $x$ 坐标:\[\sqrt{\frac{mv^2}{\alpha}}\cdot\ \left(\frac{2\sqrt{2}\alpha x}{4\alpha+\sqrt{2}mxv^2}\right)^{3 / 2} \tanh ^{-1}\left(\sqrt{\frac{\sqrt{2}mxv^2}{4\alpha+\sqrt{2}mxv^2}} \right)+\left(\frac{ x^2m}{8\alpha+2\sqrt{2}mxv^2}\right)v^2-x\]时间旅行器横 $y$ 坐标:\[\left(\sqrt{\frac{mv^2}{\alpha}}\cdot\ \left(\frac{2\sqrt{2}\alpha x}{4\alpha+\sqrt{2}mxv^2}\right)^{3 / 2} \tanh ^{-1}\sqrt{\frac{\sqrt{2}mxv^2}{4\alpha+\sqrt{2}mxv^2}} \right)+\left(\frac{ x^2m}{8\alpha+2\sqrt{2}mxv^2}\right)v^2\]质点最终速度沿 $x$ 正向,大小为 $v$ .
-
- 要想验证基本粒子的弱子模型是否正确,需要设法通过实验直接或间接地探测到弱子的存在,比如可以从基本粒子中分离出弱子,或者能由弱子结合生成基本粒子,但是目前的实验均无法找到单独存在的弱子,因此弱子理论目前仅仅是一个模型,实验上还未能验证其正确性. 实验上存在的困难可能是弱子的尺度太小了,或者说是弱相互作用力的尺度太小了,要想探测到弱子很可能需要借助弱相互作用力,因此难以探测到.
- 相对论中能量和动量的关系式为:\[E^2=p^2c^2+m_0^2c^4\]当弱子的能量$E$恒定时,其动量越小(也就是速度越小),质量就越大. 由此可知,弱子是通过降低运动速度的方式来获得固有质量的.
\[q_{\omega^\star}=\frac{2}{3}e\]- 电子的固有质量一般远大于光子,如果某粒子由 $2$ 个弱子构成,那么这 $2$ 个弱子之间的相互作用力只能沿着它们的连线方向,这将导致弱子运动的平均速率接近甚至达到光速 $c$ ,根据前面分析的粒子获得固有质量的机制, $2$ 个弱子构成的粒子将不太可能具有较大的质量,因此两个弱子可能构成光子,但不可能构成电子.
\[F(r)=6Kg_w^2\exp\left(-kr\right)\left(\frac{1}{r^2}+\frac{k}{r}-\frac{4k^2B}{\rho}r\exp\left(-kr\right)\right)\]分析函数 $F(r)$ 的数学性质,容易发现其定义域是 $r>0$ ,当 $r\to0$ 和 $r\to+\infty$ 时 $F(r) > 0$ ,弱相互作用表现为排斥力;存在一个区间 $\left(r_1,r_2\right)$ ,在这个区间内 $F(r) < 0$ ,弱相互作用表现为吸引力。因此,电子周围存在一个“球壳”,光子可以被弱相互作用束缚在这个球壳内,这就是电子的光子云模型. 当电子做变速运动时,如果以电子为参考系,电子的光子云中的光子会受到一个惯性力的作用,从而脱离弱相互作用的束缚,这就是电子在做变速运动时产生轫致辐射的原因;空间中处处遍布着光子,电子好似浸泡在“光子海”中,当光子与电子的距离在区间 $\left(r_1,r_2\right)$ 内时,将被弱相互作用力捕获,这就是电子吸收光子的原因.- 可以认为温度的物理意义是系统能级的分布(即每个能级上的粒子数). 分析过程略.
\[S=k\left(\sum_na_n+\sum_n\frac{\varepsilon_n}{kT}a_n\right)=k\sum_na_n\left(1+\frac{\varepsilon_n}{kT}\right)\]
-
- 光的干涉是指因两束光波相遇而引起光的强度重新分布的现象. 发生条件包括:1.频率相同;2.光矢量的振动方向相同;3.在相遇处两束光的相位差恒定.
\[-r_1=t_1=\sqrt{\frac{2}{5}}\] \[r_2=t_2=\sqrt{\frac{{3}}{5}}\]
\[\frac{3}{2}\]
\[0.75\]
\[2.82\]
-
\[R_{AB}=\frac{\sqrt{17}-3}{2}R\]
\[R_{AC}=\frac{\sqrt{17}+1}{8}R\]
\[R_{AB}=\frac{5-\sqrt{17}}{2}R\]
\[R_{AB}=\frac{\sqrt{7}-1}{3}R\]
\[R_{AO}=\frac{2\sqrt{7}+1}{18}R\]接通BC后的结果仍为上值.
\[R_{AB}=0.5306 R\]