第八届线上物理竞赛试题和参考答案发布
发布时间:2024-03-17 20:00:00
大家好!今天发布第八届线上物理竞赛试题和参考答案。由于解析属于OPhO参与奖的一部分,因此我们公开发布的内容中不含解析。
您可以点击下方按钮下载pdf格式的试题和参考答案文件,也可以直接在本网页上阅读试题和参考答案。我们之后会陆续发布更早的OPhO的试题和参考答案,敬请关注!
特别提醒:此处pdf文件版的第八届线上物理竞赛预赛试题、第八届线上物理竞赛预赛参考答案、第八届线上物理竞赛决赛试题、第八届线上物理竞赛决赛参考答案均使用署名-非商业性使用-禁止演绎4.0国际许可协议进行许可,请务必遵守此协议!
第八届OPhO预赛试题
单选题:在每道题的4个选项中,有且仅有1个选项是符合题意的,第1-10题每题5分,第11-20题每题10分
- 国际单位制中功的单位是______.
- $ \mathrm{N} $ (牛顿)
- $ \mathrm{J} $ (焦耳)
- $ \mathrm{W} $ (瓦特)
- $ \mathrm{Pa} $ (帕斯卡)
- 一个人的身高的数量级为______.
- $ 10^{0}\mathrm{m} $
- $ 10^{1}\mathrm{m} $
- $ 10^{2}\mathrm{m} $
- $ 10^{3}\mathrm{m} $
- 下列微观粒子中不携带电荷的是______.
- 电子
- 质子
- 中子
- 离子
- 考虑一质量为 $ m $ 的某物体,若令其温度升高 $ \Delta T $ 需要向它传递的热量为 $ Q $ ,则该物体的比热容为______.
- $ \frac{ \Delta T}{Q} $
- $ \frac{Q}{\Delta T} $
- $ \frac{m \Delta T}{Q} $
- $ \frac{Q}{m\Delta T} $
- 地球上千米长度的火花放电称为闪电,关于闪电,下列叙述不正确的是______.
- 闪电伴随着电能转化为其它形式的能量如内能
- 闪电发生时,雷云与雷云之间、雷云与地面之间有电流通过
- 每次闪电发生过后雷云携带的电荷通常会减少
- 通常情况下空气属于导体而非绝缘体,因此闪电才会得以发生
- 如图所示,物块A与B在两面竖直墙间静止,两物块受到重力分别为 $ G_\mathrm{A} $ 与 $ G_\mathrm{B} $ ,若墙面对A的静摩擦力大小为 $ f $ ,则墙面对B的静摩擦力大小为______.
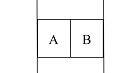
- $ G_\mathrm{A}+G_\mathrm{B}+f $
- $ G_\mathrm{A}-G_\mathrm{B}-f $
- $ G_\mathrm{A}-G_\mathrm{B}+f $
- $ G_\mathrm{A}+G_\mathrm{B}-f $
- 考虑如图所示的一块圆形玻璃板,一束包含红绿蓝三种颜色的光自空气中从玻璃板侧面入射进入板内,再从玻璃板的侧面出射,入射光线不在玻璃板任一直径上,则三种颜色的光在玻璃板中行走路程最长的是______.
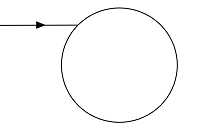
- 红光
- 绿光
- 蓝光
- 一样
- 对于烧开水的过程,下列叙述正确的是______.
- 若加热设备的温度始终低于水的沸点,则永远不可能将水烧开
- 若使用某温度大于水的沸点且温度恒定的热源与水接触将水烧开,则当水温达到沸点后仍会继续升高,因为水与热源之间依旧存在温度差
- 若用电热器烧水,水从温度低于沸点到温度达到沸点的过程中,水吸收的热量恰好等于电能的消耗(假设热量不会散失到周围环境中,不计电热器的导线的电能损耗)
- 在水烧开后,可以看到空气中弥漫着白色的“水雾”,这些水雾是水汽化后形成的水蒸气
- 如图所示是径向环形磁铁,其左半边是N极,右半边是S极,若该磁铁沿虚线断裂开分成4部分,则A与B分别是______.
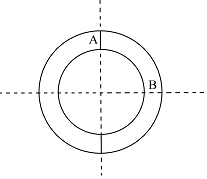
- N极;N极
- S极;S极
- N极;S极
- S极;N极
- 考虑如图所示的曲面静止于水平地面,现给曲面一向左的初速度,同时在曲面顶端相对曲面静止释放一小球,忽略一切摩擦,则以地面看来小球在下滑过程中的机械能______.
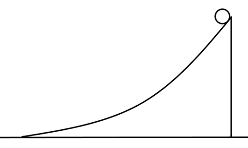
- 减小
- 增大
- 不变
- 无法判断
- 有一辆车作直线运动,中途不改变运动方向,若该车在前一半时间的平均速度大小是后一半时间平均速度大小的一半,且在前一半路程的平均速度大小是后一半路程的平均速度大小的一半,下列关于此车在这段时间内的运动叙述正确的是______.
- 整个过程的平均速度等于前一半路程的平均速度的3/2
- 整个过程的平均速度等于后一半时间的平均速度的4/9
- 前一半时间的平均速度等于前一半路程的平均速度的8/9
- 前一半路程的平均速度等于后一半时间的平均速度的9/32
- 如图所示,一个空气中焦距为 $ f $ 的厚度不计的平凸透镜浮在水面上,凸透镜折射率为 $ n_1 $ ,水的折射率为 $ n_2 $ ,空气折射率为 $ 1 $ ,则垂直向下入射的平行光通过凸透镜后在水中聚焦的位置到水面的距离为______(光线傍轴,即可使用小角近似 $ \tan x\approx\sin x \approx x $ ).
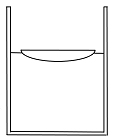
- $ \frac{n_1-n_2}{n_1-1}f $
- $ \frac{n_1-1}{n_1-n_2}f $
- $ \frac{n_1-n_2}{n_2(n_1-1)}f $
- $ \frac{n_2(n_1-1)}{n_1-n_2}f $
- 考虑一透明板,其透光率为 $ \eta $ ,其反射率为 $ 1-\eta $ ,板的两个表面性质相同,则 $ N $ 块这样的 板叠放在一起的透光率为______.
- $ \frac{\eta}{N} $
- $ \eta^N $
- $ \frac{\eta}{N-(N-1)\eta} $
- $ \frac{\eta(1-\eta)}{N-\eta^N} $
- 考虑地面固定一个足够大的不光滑的斜面,斜面同水平面夹角为 $ \theta $ , 其上动摩擦因数与静摩擦因数同为 $ \mu=\tan\theta $ ,如图所示,一质点初始时拥有平行于斜面和水平面的速度 $ v $ ,则在足够长时间后质点的速度大小为______.
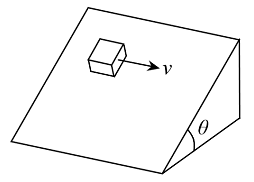
- $ 0 $
- $ \frac{v}{2} $
- $ v\cos\theta $
- $ v $
- 考虑在均匀磁场中一金属导体圆环,圆环平面垂直于磁场,若圆环绕其轴以恒定角加速度 $ \alpha $ 加速转动,圆环角速度方向始终与磁场方向相同,已知电子质量为 $ m $ ,电荷量为 $ -e $ ,若在一段时间 $ t $ 内圆环内没有电流,则这段时间磁场的磁感应强度的变化为______.
- 均匀增加 $ \frac{{2m}\alpha t}{e} $
- 均匀增加 $ \frac{{4m}\alpha t}{e} $
- 均匀减少 $ \frac{{2m}\alpha t}{e} $
- 均匀减少 $ \frac{{4m}\alpha t}{e} $
- 假设物体发出热辐射的功率与其热力学温度的 $ 4 $ 次方成正比,比例系数只与该物体的大小、形状和材料种类 相关;两个物体之间发生热传导的功率与它们之间的热力学温度之差的绝对值成正比,比例系数只与这两个物体的大小、形状和材料种类相关. 考虑组装如图所示的电路来做实验,电源的电动势恒为 $ E $ ,内阻不计;两个定值电阻 $ R_1 $ 、 $ R_2 $ 的大小、形状和 材料种类均相同,阻值均为 $ R $ 且始终保持恒定; $ L $ 是一个小灯泡,它的发光情况仅与它两端的电压有关,它到两个定值电阻的距离相等;实验场所的环境温度恒定且无风,导线均为理想导线. 实验开始前,所有开关都处于断开状态,所有实验仪器均与环境温度相同,现用很薄的黑色橡胶套套住 $ R_1 $ ,用很薄的白色橡胶套套住 $ R_2 $ ,实验开始后,闭合开关 $ S_1 $ . 下列叙述正确的是______.
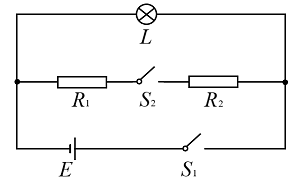
- 闭合开关 $ S_1 $ 足够长时间后,再闭合开关 $ S_2 $ ,足够长时间后, $ R_1 $ 外橡胶套的温度比 $ R_2 $ 外橡胶套高
- 闭合开关 $ S_1 $ 足够长时间后, $ R_1 $ 外橡胶套的温度比 $ R_2 $ 外橡胶套高,其原理与夏天穿 黑色衣服会比穿白色衣服更容易热不同
- 闭合开关 $ S_1 $ 足够长时间后, $ R_1 $ 外橡胶套的温度比 $ R_2 $ 外橡胶套高,主要原因并不是 $ R_1 $ 及其橡胶套吸收热辐射的功率与发出热辐射的功率之差大于 $ R_2 $ 及其橡胶套
- 闭合开关 $ S_1 $ 后,闭合开关 $ S_2 $ ,此后某时刻灯泡 $ L $ 的灯丝突然熔断了,又过了足够长 时间后, $ R_1 $ 外橡胶套的温度比 $ R_2 $ 外橡胶套高, $ R_1 $ 与 $ R_2 $ 单位时间内产生的焦耳热均为 $ \frac{E^2}{4R} $
- 考虑真空中一半径为 $ R $ 的带电导体球,在球外某处有一和导体球电量相同的点电荷,若点电荷和导体球间静 电力为0,则点电荷到导体球心的距离为______.
- $ \frac{R}{2}+\frac{\sqrt{5}}{2}R $
- $ \frac{R}{3}+\frac{\sqrt{6}}{3}R $
- $ R+\frac{\sqrt{6}}{3}R $
- $ R+\frac{\sqrt{6}}{4}R $
- 一辆汽车在空气中爆炸时的平均爆炸冲击功率为 $ P $ ,现假设有另一辆烧同种汽油的卡车,汽油含量为汽车的4倍,其质量为汽车的2倍,两辆车的密度相同,则卡车在空气中爆炸时的平均爆炸冲击功率为______和______.
- $ 2.82P $
- $ 4.49P $
- $ 20.78P $
- $ 45.03P $
- 现有某种液体中分布着某种理想气体的气泡,所有气泡均静止,气泡的体积、压强、温度均相同,单位质量该种理想气体的热容为 $ c $ ,其绝热指数(热容比)近似为1. 若某一气泡受扰动后获得向上的初速度 $ v $ ,当其遇到另一气泡与其融合 成一更大的气泡后继续匀速上浮,而气泡体积平衡的条件是压强为一确定值,气泡未平衡时的膨胀可视为绝热膨胀. 忽略气泡与液体之间的热交换,忽略重力、浮力、黏滞阻力对气泡速度的影响,气泡在每次与下个气泡融合前均已达到压强平衡,则第一个气泡融合了 $ n $ 个气泡且平衡后的温度与开始相比升高了______.
- $ \frac{v^2}{4(n+1)^2c} $
- $ \frac{nv^2}{4(n+1)^2c} $
- $ \frac{v^2}{2(n+1)^2c} $
- $ \frac{nv^2}{2(n+1)^2c} $
- 若将地球视为质量分布均匀的理想球体,某天正午一身高为 $ d $ 的人直立时影子长度为 $ l_1 $ ,此人沿此时影子所在的“直线”行走了路程 $ s $ ,次日正午此人直立时影子长度为 $ l_2(l_1,l_2\geqslant0 $ 且 $ l_1\neq l_2 $ ),已知影子是由太阳光照射此人形成的. 若已知在距地面高为 $ h $ 的轨道上绕地球做匀速圆周运动的人造卫星的周期为 $ T $ ,万有引力常数为 $ G $ ,此人想用上述信息估算地球密度,下列叙述正确的______.
- 利用题干信息估算地球密度时,无法考虑地球大气对太阳光的折射,也无法考虑季节因素.前者可能造成 估算结果有较大的误差,而后者产生的误差则非常小. 此外,为得到尽可能准确的估算结果,“正午”时间应当是指某一时区的标准时间的正午,而不应是当地的正午(即地方时)
- 人造卫星能够稳定地绕地球做匀速圆周运动而不掉落到地面,是因为人造卫星受到了地球施加的重力的作用. 若地球半径为 $ R $ ,地球质量为 $ M $ ,则人造卫星上质量为 $ m $ 的仪器受到的重力大小是 $ G{Mm}/{\left(R+h\right)^2} $ (不考虑地球外其它天体对人造卫星的影响)
- 估算地球密度为 $ \rho=\frac{{3\pi\left[1+({h}\alpha/{s}\right)]^3}}{GT^2} $ ,而 $ \alpha=\arctan{\frac{d\left|l_1-l_2\right|}{d^2+l_1l_2}} $
- 估算地球密度为 $ \rho=\frac{{3\pi\left[1+({h}\alpha/{s}\right)]^3}}{GT^2} $ ,而当 $ \arctan{\frac{d\left(l_1+l_2\right)}{d^2-l_1l_2}}\geqslant0 $ 时 $ \alpha=\arctan{\frac{d\left(l_1+l_2\right)}{d^2-l_1l_2}} $ ,当 $ \arctan{\frac{d\left(l_1+l_2\right)}{d^2-l_1l_2}}< 0 $ 时 $ \alpha=\pi+\arctan{\frac{d\left(l_1+l_2\right)}{d^2-l_1l_2}} $
第八届OPhO预赛参考答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | A | C | D | D | D | C | A | B | D | C | D | C | B | A | C | A | B | D | A |
第八届OPhO决赛试题
解答题:从下列四道选题中任选两道作答,每道题75分,多做的部分不给分
- 我们将分析刚体动力学中的一个佯谬,卡罗尔佯谬. 考虑如图左图所示的质量为 $ m $ 的匀质刚性细杆 被约束在一个光滑同轴圆桶中,圆筒内外半径差为 $ r_{\text out}-r_{\text in} $ 且等于杆长 $ l $ ,圆筒竖直放置,杆的中点到 圆筒中轴距离为 $ r $ . 初始时杆平行于地面静止 $ (\text{A}^\prime \text{B}^\prime) $ . 约束使得该系统的自由度为1,可以使 用图中标识的角度 $ \theta $ 描述.

- 试求该杆绕过其中点,垂直于杆的轴的转动惯量. (3分)
- 试求该杆绕圆筒中轴的转动惯量. (4分)
- 基于角动量定理列出用 $ \theta $ 及其导数表达的运动方程(不必求解). (6分)
- 基于动量定理列出用 $ \theta $ 及其导数表达的运动方程(不必求解). (6分)
- 试证明(3)与(4)中的方程联立后无解. (8分)
- 对(5)中出现佯谬的一个解释是AB两点的约束反力必须存在垂直于杆的分量. 现考虑杆比圆筒稍长的情况, 即杆长 $ l=r_{\text out}-r_{\text in}+\varepsilon $ ,如图右图所示,C是杆的中心, $ \theta $ 现是OC与竖直线的夹角,用 $ \theta_1 $ 与 $ \theta_2 $ 分别表示OA和OB与竖直线的夹角. 已知现在杆对圆筒中轴的转动惯量为 $ J $ ,试求A、B两点筒壁对杆的力. (15分)
- 试求圆筒对杆的合力垂直于OC及平行于OC的分量大小,证明二者均与 $ \varepsilon $ 无关. (15分)
- 通过取 $ \varepsilon\rightarrow 0 $ ,给出(3)(4)(5)中出现佯谬的解释. (18分)
- 理想气体的四种常见准静态过程为等体过程、等压过程、等温过程、绝热过程. 但是对于分子数可变的理想气体,其具有更多可能的准静态过程:考虑有一个气缸,其上开有一小孔,外界与缸内是同种理想气体,而气体可以从小孔上充入或泄出,这样的准静态过程称为充气过程. 假设外界压强和温度恒定,温度恒为 $ T_0 $ ,每单位物质的量此种理想气体的定体热容为 $ c_v $ ,定压热容为 $ c_p $ ,热容比 $ \frac{c_p}{c_v}=\gamma $ ,气体普适常数为 $ R $ . 考虑以下6种不同的充气过程.
- 写出理想气体状态方程、理想气体的内能公式以及热力学第一定律的内容. (3分)
- 等体绝热充气过程:气缸体积恒定,与外界绝热,试推导这种过程的方程(恒定不变的量可以用 $ C $ 表示,例如一定量理想气体绝热过程的方程为 $ pV^{\gamma}=C $ ). (12分)
- 等压绝热充气过程:气缸压强恒定,与外界绝热,试推导这种过程的方程.(12分)
- 等体等温充气过程:气缸体积恒定,温度恒为 $ T $ ,充入理想气体物质的量为 $ \Delta n $ ,试求气缸内气体放出的热量. (12分)
- 等压等温充气过程:气缸压强恒定,温度恒为 $ T $ ,充入理想气体物质的量为 $ \Delta n $ ,试求气缸内气体放出的热量. (12分)
- 等体等压充气过程:气缸体积恒定为 $ V $ ,气缸压强恒定为 $ p $ ,充入理想气体使气缸内 气体物质的量从 $ n_0 $ 变为 $ n $ ,试求气缸内气体放出的热量. (12分)
- 等温绝热充气过程:气缸温度恒为 $ T $ ,与外界绝热,试推导这种过程的方程. (12分)
- 如图所示,两个共球心的空心匀质导体球,内导体球内外半径分别为 $ R $ 、 $ 2R $ ,外导体球内外半径分别 为 $ 3R $ 、 $ 4R $ . 导体球的电阻率均为 $ \rho $ ,现在用无电阻的球面形状电刷将两个导体球的内外面全部均匀包覆,并将外导体球的内表面的电刷与内导体球的外表面的电刷用阻值为 $ r $ 的导线连接,再使用理想导线将一电动势为 $ E $ ,内阻为 $ r $ 的 直流电源的正负极分别接在外导体球的外表面电刷和内导体球的内表面电刷上,并将电源负极接地. 假设导线与电刷、电刷与导体球表面之间接触良好. 现闭合开关 $ S $ ,直到电路达到稳定. 规定无穷远为电势零点. 静电力常数为 $ k $ .
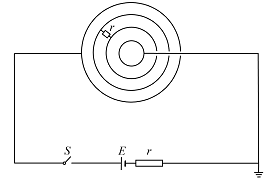
- 试判断该电路中两个导体球之间是串联还是并联. (3分)
- 内导体球的内表面上是否带电?若带电,带何种符号的电荷?阐释原因. (6分)
- 试求内导体球在该电路中的电阻. (9分)
- 试求通过电源的电流及电源两端的电压. (9分)
- 试求外导体球内表面上的电势. (10分)
- 试求内导体球内表面两侧的电场. (12分)
- 试求外导体球外表面所带的电荷. (12分)
- 试求直流电源的电功率. (14分)
- 在一个惯性系中考虑某静止质量为 $ m_0 $ 的质点在竖直向下恒定的力 $ F $ 作用下的运动. 质点相对惯性系初速度为 $ v_0 $ ,讨论全部在该惯性系中进行,需计及狭义相对论效应. 真空光速为 $ c $ .
- 若质点初速度方向竖直向上,试求惯性系中质点到达最高点处的高度及用时. (4分)
- 若质点初速度方向水平,试求质点下落 $ h $ 后的速度大小. (6分)
- 在(2)的条件下,试求质点在惯性系中下落的用时. (6分)
- 在(2)的条件下,试求质点的位移与水平方向的夹角及质点的速度与水平方向的夹角. (13分)
- 若质点初速度方向斜向上,其初速度与水平方向的夹角为 $ \theta $ ,试求其能到达的最高点高度. (13分)
- 在(5)的条件下,试求质点轨迹最高点处的曲率半径. (14分)
- 若质点初速度方向斜向上,且初速度 $ v_0\rightarrow c $ ,定义质点回到与出发点相同高度时与出发点的距离为射程. 若欲使质点射程最远,试求初速度与水平方向所呈角度. (19分)
第八届OPhO决赛参考答案
-
- \[J_c=\frac{1}{12} m l^2\]
- \[J=\frac{1}{12} m l^2+mr^2\]
- \[\left(\frac{1}{12} m l^2+mr^2\right)\ddot\theta=-m g r \sin \theta\]
- \[m r \ddot{\theta}=-m g \sin \theta\]
- 联立(3)(4)的两个方程可以给出:\[J \ddot{\theta}=0\]即 $ \dot{\theta}=\text{Const} $ ,但是考虑到初始条件 $ \dot{\theta}(0)=0 $ ,该杆将不会运动. 但依照受力分析,初始时杆不应当平衡. 故矛盾.
- \[\begin{aligned}& F_A=\frac{mg}{J}\frac{(J-mr^2) \sin \theta_2-3 mr^2 \cos \theta \sin \left(\theta-\theta_2\right)}{\sin \left(\theta_2-\theta_1\right)} \\& F_B=\frac{mg}{J} \frac{(J-mr^2) \sin \theta_1-3 mr^2 \cos \theta \sin \left(\theta-\theta_1\right)}{\sin \left(\theta_1-\theta_2\right)}\end{aligned}\]
- 垂直于OC的分量是:\[T=\left(1-\frac{m r^2}{J}\right) m g \sin \theta\]平行于OC的分量是:\[T=\left(1+\frac{2m r^2}{J}\right) m g \cos \theta\]二者均与 $ \varepsilon $ 无关.
- 当我们取极限 $ \varepsilon\rightarrow 0 $ 时, $ \sin(\theta_2-\theta_1)\approx \theta_2-\theta_1\propto \sqrt{\epsilon} $ ,反观(6)中 $ F_A, F_B $ 的表达式,这个极限导致分母的发散,即 $ F_A,F_B $ 会按 $ \varepsilon^{-1/2} $ 发散,趋于无穷,于是实际上这样的约束根本不可能被实现. 至此,佯谬得到解决.
-
- 理想气体状态方程: $ pV=NkT $ , $ N $ 为理想气体分子数. 理想气体内能: $ U=nc_vT $ . 热力学第一定律:物体内能的增加等于物体吸收的热量和对物体所做的功的总和.
- \[p\left(\frac{\gamma T_0}{T}-1\right)=\text{常数}\]
- \[p\left(\frac{ T_0}{T}-1\right)=\text{常数}\]
- \[\Delta Q=c_vT\Delta n-c_pT_0\Delta n\]
- \[\Delta Q=c_p(T-T_0)\Delta n\]
- \[\Delta Q=-pV\frac{c_v}{R}\ln n-c_pT_0\Delta n\]
- \[pV^{\frac{\gamma T_0-2T}{\gamma T_0-T}}=\text{常数}\]
-
- 串联.
- 带负电. 因为电路稳定后在内导体球内必定存在由外向内的传导电流,而导体球有电阻,所以内导体球内外表面必存在电势差,外表面电势高于内表面,而由于内导体球外表面的电荷、外导体球的电荷都是均匀分布,不在内导体球内部产生电场,故内导体球内表面的电荷必须产生自外指向内的电场,所以内表面带负电.
- 电阻为:\[\frac{\rho}{8\pi R}\]
- \[I=\frac{48\pi RE}{96\pi Rr+7\rho}\]\[U=\frac{48\pi Rr+7\rho }{96\pi Rr+7\rho}E\]
- 电势为:\[\frac{48\pi Rr+6\rho}{96\pi Rr+7\rho}E\]
- 电场强度大小为:\[\frac{32\rho E}{(96\pi Rr+7\rho)kR}\]方向由外向内.
- \[Q=\frac{(192\pi Rr+136\rho)RE}{k(96\pi Rr+7\rho)}\]
- \[P=\frac{48\pi RE^2}{96\pi Rr+7\rho}\]
-
- \[h=\left(\frac{1}{\sqrt{1-\frac{v_0^2}{c^2}}}-1\right)\frac{c^2}{F}\qquad \quad t=\frac{m_0v_0}{F\sqrt{1-\frac{v_0^2}{c^2}}}\]
- \[v=c\sqrt{1-\left(\frac{m_0c^2\sqrt{c^2-v_0^2}}{Fh\sqrt{c^2-v_0^2}+m_0c^3}\right)^2}\]
- \[t=\sqrt{\frac{h^2}{c^2}+\frac{2m_0hc}{F\sqrt{c^2-v_0^2}}}\]
- \[\theta_r=\mathrm{arccot} \left[\frac{m_0v_0c^2}{Fh\sqrt{c^2-v_0^2}}\text{arsinh}\left(\frac{F}{m_0c}\sqrt{1-\frac{v_0^2}{c^2}}\sqrt{\frac{h^2}{c^2}+\frac{2m_0hc}{F\sqrt{c^2-v_0^2}}}\right)\right]\]\[\theta_v=\arctan \left[\left(\frac{F^2(c^2-v_0^2)h^2}{m_0v_0^2c^4}+\frac{2Fh\sqrt{c^2-v_0^2}}{m_0v_0^2c}\right)^{1/2}\right]\]
- \[h=\frac{m_0c^3-\sqrt{m_0^2c^6-m_0^2v_0^2 c^4\sin^2\theta}}{F\sqrt{c^2-v_0^2}}\]
- \[\rho=\frac{m_0}{F}\frac{c^2v_0^2(1-\sin^2\theta)}{\sqrt{(c^2-v_0^2\sin^2\theta)(c^2-v_0^2)}}\]
- $ 56.5^\circ $