第七届线上物理竞赛试题和参考答案发布
发布时间:2024-06-07 20:00:00
大家好!今天发布第七届线上物理竞赛试题和参考答案。由于解析属于OPhO参与奖的一部分,因此我们公开发布的内容中不含解析。
您可以点击下方按钮下载pdf格式的试题和参考答案文件,也可以直接在本网页上阅读试题和参考答案。我们之后会陆续发布更早的OPhO的试题和参考答案,敬请关注!
特别提醒:此处pdf文件版的第七届线上物理竞赛预赛试题、第七届线上物理竞赛预赛参考答案、第七届线上物理竞赛决赛试题、第七届线上物理竞赛决赛参考答案均使用署名-非商业性使用-禁止演绎4.0国际许可协议进行许可,请务必遵守此协议!
第七届OPhO预赛试题
单选题:在每道题的4个选项中,有且仅有1个选项是符合题意的,每题5分
- 首位发现金星具有圆缺位相变化的是______.
- 第谷(Tycho Brahe)
- 托勒密(Claudius Ptolemy)
- 伽利略(Galileo Galilei)
- 牛顿(Isaac Newton)
- 只有一个中子的“原子”属于零号元素,这种核素与氕核的核素互为______.
- 同位素(Isotope)
- 同核异能素(Isomer)
- 同量异位素(Isobar)
- 同中子异位素(Isotone)
- 以下波动不需要介质就可以传播的是______.
- 自旋波(spin wave)
- 引力波(gravitational wave)
- 零声波(zero sound)
- 等离子体波(plasma wave)
- 假设摒弃现有牛顿力学的概念,并试图从运动学中引入的加速度矢量 $ \vec{a} $ 和牛顿第一定律重新建立“牛顿第二定律”,即引入相互作用力 $ {F} $ 并给出其与 $ \vec{a} $ 的定量关系,下列说法不正确的是______.
- 因为描述相互作用的力 $ F $ 之度量尚未确立,所以可以定义力矢量,使得对于同一物体而言,有 $ |\vec{F}|\propto |\vec{a}|^2 $
- 若力矢量 $ \vec{F} $ 的度量确定为 $ \vec{F}\propto \vec{a} $ ,但是不同物体惯性质量的度量还 未定义,我们可以定义一个物体的惯性质量 $ m $ ,使 $ \vec{F}=km^2 \vec{a} $ , $ k $ 是与力所选单位有关的常数
- 当且仅当力 $ \vec{F} $ 的度量确定为 $ \vec{F}\propto \vec{a} $ ,力的合成才满足矢量和的平行 四边形法则
- 若定义相互作用力为一矢量 $ \vec{F} $ ,则可以定义其方向不在物体加速度 $ \vec{a} $ 所在直线上
- 使用某测量仪器测量某待测量若干次,每一次测量都比前一次测量精度更高,得到一组测量数据 $ v_i $ ;则随 着测量次数不断增加及精度的不断提高,下列误差不可能减小的是______.
- 测量值 $ v_i $ 的绝对误差
- 测量值 $ v_i $ 的相对误差
- 测量值 $ v_i $ 的示值误差
- 测量数据组 $ \{v_i\} $ 的标准误差
- 在国际单位制中,光速 $ c $ 的单位为 $ \mathrm{m/s} $ ,约化普朗克常数 $ \hbar $ 的单位为 $ \mathrm{J\cdot s} $ ;在自然单位制中,光速和约化普朗克常数规定为 $ c=\hbar=1 $ . 在自然单位制中下列物理量与时间具有相同单 位的是______.
- 压强
- 功率
- 作用量
- 转动惯量
- 在狭义相对论中,当一个物理量的取值不随所选取的惯性参考系的不同而改变,则这个物理量是标量. 以 下在狭义相对论中是标量的物理量是______.
- 动能
- 频率
- 静止质量
- 某点电场强度的大小
- 管乐器通常是均匀管. 如图所示为管风琴的半开管的纵截面图。空气自吹口吹入,形成气流喷注,在遇到 劈尖后,一部分流到管外,另一部分激发管内气体振动,发出声音. 则当该管风琴均匀发声时,图中四点声音强度最大的是______.
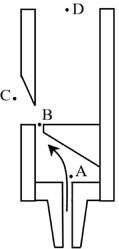
- A点
- B点
- C点
- D点
- 如图所示为竖直放置的刚性水管的纵截面图,水管横截面积恒定且很小. 现在将水管的三个管口A,B,C封堵,并在 管内注满液体水,当同时打通三个管口后,一定有水溢流出的管口是______.
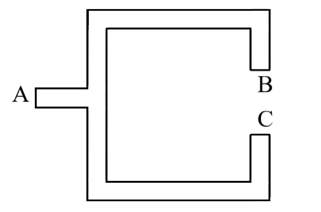
- B
- C
- A和B
- B和C
- 已知空间中有均匀的电场和磁场,现有一已知荷质比的带电粒子,可以任意初速度释放,并能且仅能在释放一瞬间对该粒子的加速度进行测量,在此之后无法得知粒子运动的信息,不计该粒子的重力. 若欲确保能够确定空间中电场及磁场的大小及方向,最少需要释放并测量粒子的次数为______.
- 2
- 3
- 4
- 5
- 我国自古就有人工制造冰的技术,庄子曰:“我得夫子之道矣,吾能冬爨鼎而夏造冰矣!”以下说法正确的是______.
- 《淮南万毕术》中记载的“取沸汤置瓮中,密以新缣,沈中三日成冰.”主要是利用水蒸发过程中吸收热量 这一原理来制造冰的
- 硝石溶于水的过程中会吸收热量,可以利用这一原理来制造冰,这一过程中水的温度从和周围环境相同变成了低于周围环境,说明在一定条件下热量可以自发地从低温物体流向高温物体,从而使得低温物体的温度更低,但这一过程是有限度的,不会无休止地进行下去
- 古人冬天将冰贮存在地窖里,到了夏天再将冰取出来给环境制冷,为了提高贮存效率,应尽可能将冰切成长方体来贮存,而不是直接贮存形状不规则的冰
- 空调、冰箱等是现代人常用的制冷设备,如果输入这些设备的电能全部用于制冷(即不计用于其他功能的电能和一些机械运作固有的电能损耗),则它们的工作效率通常与周围环境的温度无关,无论周围环境的温度如何,工作效率都不能达到 $ 100\% $
- 在量子力学中,可观测的物理量从经典物理中的实数替换为算符,两个算符 $ \hat{a} $ 和 $ \hat{b} $ 的对易式定义为 $ [\hat{a},\hat{b}]=\hat{a}\hat{b}-\hat{b}\hat{a} $ ,算符不满足乘法交换律,但是满足分配律. 若角 动量矢量的算符 $ \hat{\vec{L}} $ 的分量的对易式满足 $ [\hat{L}_x,\hat{L}_y]=\mathrm{i}\hbar\hat {L}_z $ , $ \mathrm{i} $ 是虚数单位, $ \hbar $ 是约化普朗克常数. 若 $ \hat{\vec{L}}_1 $ 和 $ \hat{\vec{L}}_2 $ 为两个粒子的角动量算符(不同粒 子的角动量算符的对易式为0),则下列属于角动量算符的是______.
- $ 2\hat{\vec{L}}_1 $
- $ \hat{\vec{L}}_1+\hat{\vec{L}}_2 $
- $ \hat{\vec{L}}_1-\hat{\vec{L}}_2 $
- $ \mathrm{i}\hat{\vec{L}}_1+\mathrm{i}\hat{\vec{L}}_2 $
- 光滑水平面上的两个质点间用一原长为 $ l $ ,劲度系数为 $ k $ 的弹簧连接,固定其中一个质点,当另一质量为 $ m $ 的质点绕固定质点以角速度 $ \omega $ 做圆周运动时,两质点间距为______.
- $ \frac{kl}{k-m\omega^2} $
- $ \frac{m\omega^2 l}{k-m\omega^2} $
- $ \frac{kl}{m\omega^2-k} $
- $ \frac{m\omega^2 l}{m\omega^2-k} $
- 在体积一定的真空绝热容器中一块干冰升华后的温度为 $ T $ (视为理想气体),则此时在该容器中再升华一块 完全相同的干冰后容器内的温度为______.
- $ T $
- $ 1.44T $
- $ 2T $
- 条件不足
- 在杨氏双缝干涉实验中,两波长为 $ \lambda $ 的相干单色点光源相距 $ d $ ,光源到成像屏的距离为 $ a(d\ll a) $ . 忽略相对论效应,当两个点光源以速率 $ v $ 靠近成像屏时(速度方向与屏垂直),屏上第 $ n $ 级亮纹的移动速率为 ______.
- $ \frac{ \lambda}{d}v $
- $ \frac{ \lambda}{a}v $
- $ \frac{ n\lambda}{d}v $
- $ \frac{ n\lambda}{a}v $
- 某行星以半径 $ R $ 围绕质量为 $ M $ 的恒星做圆周运动,现假设恒星在某一时刻的质量忽然反号 $ M\rightarrow -M $ ,不计相对论效应,则该行星被散射到无穷远的渐近速度所在直线到恒星的距离为______.
- $ \frac{\sqrt{2}}{2}R $
- $ {\frac{\sqrt{3}}{6}R} $
- $ {\frac{\sqrt{3}}{2}R} $
- $ {\frac{\sqrt{3}}{3}R} $
- 考虑如图所示的半径为 $ r $ 的半球形碗,一质点小球与碗的球心的连线与竖直方向夹角为 $ \theta(0 < \theta < \pi/2) $ . 不计机械能损耗,现给小球某一初速度,若小球能够在半球内做周期运动,且小球始终仅会触碰碗上的其中两个点,则 小球运动的周期为______.

- $ \sqrt{\frac{32r\cos\theta}{g}} $
- $ \sqrt{\frac{32r}{g}}\cos\theta $
- $ \sqrt{\frac{16r\cos\theta}{g}} $
- $ \sqrt{\frac{16r}{g}}\cos\theta $
- 一根不可伸长的轻绳跨过定滑轮,绳子一端连接质量为 $ m_1 $ 重物,另一端一质量为 $ m_2 $ 的人抓着绳子向上爬. 若重物相对地面以加速度 $ a_1(a_1 > 0) $ 加速上升,人相对地面以加速度 $ a_2(a_2 > 0) $ 加速下落,则滑轮对绳子作用力的大小为______.
- $ m_1(g+a_1)+m_2(g+a_2) $
- $ m_1(g+a_1)+m_2(g-a_2) $
- $ m_1(g-a_1)+m_2(g+a_2) $
- $ m_1(g-a_1)+m_2(g-a_2) $
- 假设有一种光学介质,其中一点的折射率只是到某固定点O距离的函数 $ n(r) $ ,并且该种介质内任一点发出的 任一条光线都构成圆,如图所示,且从一点发出所有光线都会汇聚于一点(像点). 该介质称为麦克斯韦鱼眼. 则到O点距离为 $ u $ 的点所成的像到O点的距离 $ v $ 满足关系______.
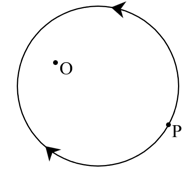
- $ uv=\text{常数} $
- $ u/v=\text{常数} $
- $ uv^2=\text{常数} $
- $ uv^3=\text{常数} $
- 光的粒子性的一面是光子,频率为 $ \nu $ 的光子具有能量 $ \varepsilon=h\nu $ 和动量 $ p=h\nu/c $ .重力常数 $ g $ 已知,现有一个质量为 $ m $ ,边长为 $ d $ 的正方体在真空中被竖直向上的激光照射,正方体底面与激光照射方向垂直,激光照射在正方体底面的中心位置,激光的平均能量密度为 $ w $ ,未被反射的光子从正方体的上面射出,反射和透射的光频 率均不变,若正方体在激光的照射下恰好静止,则正方体表面对该激光的反射率(反射光子数与入射光子数之比)为______.
- $ 1-\frac{2mg}{wd^2} $
- $ 2-\frac{mg}{wd^2} $
- $ \frac{mg}{wd^2}-1 $
- $ \frac{mg}{2wd^2} $
- 介子是由两个夸克组成的微观粒子,介子中两个夸克间通过近似为有心力场的色场束缚在一起,如图所示 ,右图夸克间的色线并不像左图的电场线一样在空间中散开,故可以近似地当作一根特殊的弦计算. 已知介子的夸克对围绕质心的转动角动量正比于夸克总能量的平方,而夸克的能量 $ E $ 与动量 $ p $ 的关系为 $ E\approx pc $ , $ c $ 为真空光速,则介子夸克对能量 $ E $ 与夸克间距离 $ r $ 的近似关系是______.
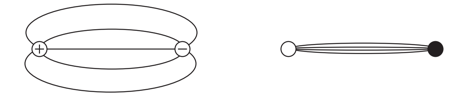
- $ E\propto r^{-1} $
- $ E\propto \ln r $
- $ E\propto r $
- $ E\propto r^{2} $
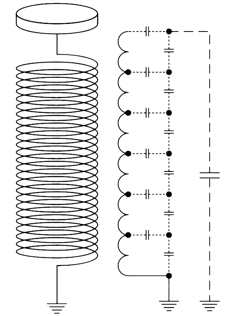
- 如图所示为特斯拉线圈的次级线圈及其等效电路图,虚线代表等效的分布电容,次级线圈由上端环状电极 放电,初级线圈与初级电容构成LC电路,并通过变压器将能量传输给次级线圈. 已知某特斯拉线圈的初级电容为 $ C $ ,次级线圈匝数 为 $ N(N\gg 1) $ ,其每两匝之间等效电容为 $ C_0 $ . 特斯拉线圈工作时,初级线圈回路与次级线圈回路达到电谐振,初级电容电压峰值为 $ V $ ,不计一切能量损耗,则环状电极与大地间的电压峰值近似为______.
- $ \sqrt{\frac{NC_0}{C}}V $
- $ \sqrt{\frac{NC}{C_0}}V $
- $ \frac{NC_0}{C}V $
- $ \frac{NC}{C_0}V $
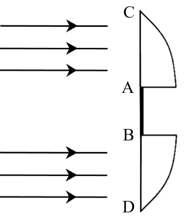
- 考虑将某一焦距为 $ f $ 的平凸透镜沿水平直径切开并垂直分开一段距离. 如图所示,AC与BD长度均为 $ R $ ,AB段长 $ d $ 且不透光. 现一束相干平行光入射,在透镜右侧放一垂直光屏,若为使屏上有明暗相间的干涉条纹,则光屏与AB的距离的 取值范围为______.
- 不会发生干涉
- $ \left(f,f+\frac{d}{R}f\right) $
- $ \left(f+\frac{d}{2R}f,f+\frac{d}{R}f\right) $
- $ \left(f+\frac{d}{2R}f,+\infty\right) $
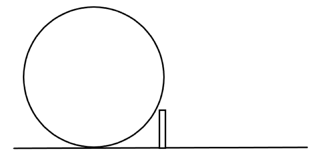
- 如图所示的半径为 $ R $ 的圆轮纯滚动地碰到一固定在地面上的障碍物,若碰撞时间足够短,且是完全弹性的, 当障碍物的高度大于______ ,则无论圆轮滚动多快都不可能越过障碍物.
- $ \frac{2-\sqrt{2}}{2}R $
- $ \frac{4-\sqrt{3}}{2}R $
- $ \frac{3-\sqrt{2}}{2}R $
- $ \frac{3-\sqrt{3}}{2}R $
- 考虑 $ N\times N(N\gg 1) $ 个正方形的网格,在中心格子释放 $ n_1 $ 个A类粒子和 $ n_2 $ 个B类粒子,若 每一步每个粒子会移动至相邻格子(粒子不能斜对角移动),粒子的移动相互独立. 经足够多的步数后,最中心格点恰有 $ x $ 个A粒子和 $ y $ 个( $ x < n_1, y < n_2 $ 且均为偶数)B粒子的概率近似是______.
- $ \frac{2^{x+y}n_{1} !n_2!}{2!\left(n_1-x\right) !\left(n_2-y\right) !}N^{-2x-2y} $
- $ \frac{2^{x+y} n_{1} !n_2!}{x !y!\left(n_1-x\right) !\left(n_2-y\right) !}N^{-2x-2y} $
- $ \frac{(2n_{1}) !(2n_2)!}{2!\left(2n_1-x\right) !\left(2n_2-y\right) !}N^{-2x-2y} $
- $ \frac{(2n_{1}) !(2n_{2})!}{x !y!\left(2n_1-x\right) !\left(2n_2-y\right) !}N^{-2x-2y} $
- 有 $ N $ 个完全相同的粒子,每个粒子衰变后,它的状态都可能变成 $ s $ 个确定的状态中的某个状态. 理论分析表明,衰变后粒子处于第 $ i $ 个状态的概率为 $ q_i $ ;实验表明,这 $ N $ 个粒子衰变后处于第 $ i $ 个状态的粒子有 $ x_i $ 个. 如果实验结果是在 $ N $ 足够大的情况下得到的,以下说法正确的是______.
- 若\[\prod_{i=1}^{s} q_i^{x_i} \frac{N !}{\prod_{j=1}^s x_j !}\]非常接近 $ 1 $ ,则足以说明理论与实验相符
- 即便若有\[\sum_{i=1}^s x_i \left(\log_2 \frac{x_i}{N}-\log_2 q_{i}\right)\gg 1,\]也不足以说 明理论与实验相符
- 若 $ s $ 不是一般的有限值,而是无穷大的,则至少存在一些状态 $ i $ ,有 $ q_i=0 $ ,如果实验 上发现有些 $ q_i=0 $ 的状态上 $ x_i\neq 0 $ ,则可以说明理论与实验不相符
- 若能够找到一个状态 $ i $ ,精确地满足 $ {x_i}/{q_i}=N $ ,则足以说明理论与实验相符
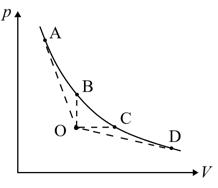
- 混合理想气体能够从某点自发地传播出去的强放热反应,称为理想气体的燃烧. 分隔未反应气体与生成气 体间的反应层称为火焰. 对于一种特定的燃烧反应,反应速率取决于气体微观参量如平均自由程、反应活化能、反应热等决定.但无论反应速率如何,当确定气体燃烧前的热力学状态 $ (p,V) $ ,生成气体的压强与体积被确定在一条 $ p $ - $ V $ 图的曲线上. 如图所示,燃烧前可燃气与助燃气的混合理想气体在O点,燃烧后可能状态处在图中的实线上,ABCD四点都在曲线上,OA与OD分别与曲线相 切,OB垂直,OC水平,则四点中对应燃烧速率最快的点是______.
- A点
- B点
- C点
- D点
- 如图所示的无穷正方形网格电路,每个最小正方形的每条边电阻都为 $ R $ ,当该无穷网格的无穷远处的节点是 同一节点时,则该网格任意一节点与无穷远节点间的等效电阻为______.

- $ \frac{2}{3}R $
- $ \frac{1}{2}R $
- $ \frac{4}{3}R $
- $ \frac{1}{6}R $
- 有两个相同的半径为 $ R $ 的导体球,各自均带电 $ Q $ .静电常数为 $ k $ . 当两球从相距无穷远缓慢靠近直到接触并达到静电平衡的过程中,两球系统的电势能改变与 $ kQ^2/R $ 的比值为______.
- $ \frac{1-\ln 2}{2\ln 2} $
- $ \frac{2-\ln 2}{2\ln 2} $
- $ \frac{1-\ln 2}{\ln 2} $
- $ \frac{2-\ln 2}{\ln 2} $
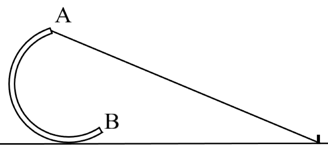
- 如图所示,水平地面上的开口朝右的半圆环上端点被弹性轻绳拉住,绳的另一端固定在右侧地面,若总能通过增大绳子与地面的夹角使圆环静止,则圆环和地面间最大静摩擦系数的最小值为______.
- $ \frac{2}{\sqrt{4+\pi^2}+1} $
- $ \frac{2}{\sqrt{4+\pi^2}+4} $
- $ \frac{2}{\sqrt{4+\pi^2}+2} $
- $ \frac{2}{\sqrt{4+\pi^2}+\pi} $
第七届OPhO预赛参考答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | C | B | D | D | D | C | B | B | A | A | B | A | A | C | D | C | B | A | D | C | B | D | A | B | A | B | A | C | D |
第七届OPhO决赛试题
解答题:从下列五道选题中任选三道作答,每道题50分,多做的部分不给分
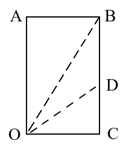
- 晶体的双折射现象指的是,光线入射到晶体中,会分解成两束相速度不同的光,它们振动方向相互垂直. 晶片便是利用双折射原理,使垂直入射的光分解为互相垂直的波速不同的光. 现考虑在一个起偏器和一个检偏器之间放置一个厚度为 $ d $ 的晶片,起偏器、检偏器和晶片相互平行,如图所示是平行于晶片的示意图,OB为起偏方向,OD为检偏方向,OA与OC是晶片中波速不 同的两个振动方向,在垂直晶片方向上两个振动方向的光的折射率分别为 $ n_1 $ 和 $ n_2 $ ,且 $ |n_1-n_2|\ll n_1 $ . 已知OB与OD夹角 $ \phi_1 $ ,OB与OC夹角 $ \phi_2 $ . 一束真空波长为 $ \lambda $ 的强度为 $ I $ 的单色入射光沿OA方向振动,并先后通过起偏器、晶片、检偏器.
- 若该晶片可以将垂直晶片入射的椭圆偏振光转化为线偏振光,求晶片厚度 $ d $ 应满足的条件. (5分)
- 若光是垂直晶片入射的,保持 $ \phi_1 $ 不变,调节 $ \phi_2 $ ,即同时转动起偏器与检偏器,分 别求为使从检偏器出射的光强最大及最小时, $ \phi_2 $ 所满足的条件,及所对应的光强. (10分)
- 如果入射光是斜入射的(保持入射面不变改变入射角),入射光与晶片的法线方向夹角为 $ \theta $ ,试求从晶片出射的两束光的相位差. (15分)
- 在(3)的条件下,如果 $ n_1-n_2=C\sin^2 \chi $ , $ C $ 是常数, $ \chi $ 是晶片内部两束光与 光轴方向(沿此方向 $ n_1=n_2 $ )的平均夹角,试求出射光的等相位面的形状. (20分)
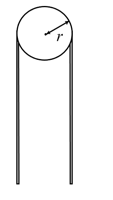
- 如图所示,一根长度 $ L $ ,线质量密度 $ \lambda $ 的不可伸长绳子跨在半径为 $ r $ 的钉子上.
- 忽略钉子上的摩擦,若 $ r $ 不可忽略,试求静止状态绳子内张力的取值范围. (5分)
- 忽略钉子上的摩擦,且 $ r/L\rightarrow 0 $ . 初始时绳子静止且左侧末端比右侧末端高 $ x(x \ll L) $ ,试求从初始时刻到向上运动的一侧的绳子末端与钉子圆心高度齐平的用时,以及这个过程钉子对绳子的平均支持力. (12分)
- 忽略钉子上的摩擦,若 $ r $ 不可忽略,初始时绳子静止且左侧末端比右侧末端高 $ x(x \ll L) $ ,试求从初始时刻到向上运动的一侧的绳子末端与钉子圆心高度齐平的用时,以及这个过程钉子对绳子的平均支持力. (15分)
- 若 $ r $ 不可忽略,绳子与钉子的最大静摩擦系数及滑动摩擦系数均为 $ \mu $ ,现改变两端绳子高度差,若绳子能够静止,试求两端绳子末端高度差的极限值. (18分)
- 在真空中建立右手三维直角坐标系 $ \mathrm{O}xyz $ .有沿 $ z $ 轴正方向的在空间上均匀分布的磁场,磁感 应强度 $ \vec{B}=B_0\hat{e}_z $ ,其中 $ B_0 > 0 $ , $ \hat{e}_x $ 、 $ \hat{e}_y $ 、 $ \hat{e}_z $ 分别表示沿 $ x $ 、 $ y $ 、 $ z $ 轴正方向的单位矢量.有一个很细的起初不带电且无电流的导体圆环,质量为 $ m $ 且分布均匀,半径为 $ r $ , 电阻为 $ R $ ,电感为 $ L $ ,将其静止置于空间中,其圆心被固定于坐标原点(用于固定的结构不会影响空间中的磁场和导体圆环中的电流,且与导体圆环之间没有摩擦力),一条直径与 $ x $ 轴重合.定义逆着 $ x $ 轴正方向看去,从 $ \hat{e}_z $ 逆时针旋转到与导体圆环的一条直径重合时,转过的角度用 $ \theta $ 表示, $ 0\leqslant\theta < \pi $ .不计重力,不计感生电流产生的磁场 对外磁场的影响,不考虑相对论效应,导体圆环不可形变.
- 分别求当 $ \theta=0 $ 和 $ \theta={\pi}/{2} $ 时通过导体圆环的磁通量. (4分)
- 求通过导体圆环的磁通量关于 $ \theta $ 的函数表达式,并由此判断当 $ \theta $ 取何值的时候,导体圆环内可能产生感生电流,并判断所产生感生电流的方向. (6分)
- 若 $ \theta={\pi}/{2} $ , $ B_0 $ 随时间 $ t $ 不断增大, $ B_0=kt $ , $ k > 0 $ 且为常数 ,求从 $ t=0 $ 时刻起导体圆环中产生的总焦耳热随时间变化的表达式. (9分)
- 若 $ \theta=0 $ , $ B_0 $ 是与时间无关的常数,导体圆环的电阻 $ R=0 $ . 某时刻(记此时的时间 $ t=0 $ )在导体圆环与 $ z $ 轴正半轴相交的质点处施加一个沿 $ y $ 轴负方向的瞬时冲量,使该质点获得速度 $ \vec{v}_0=-v_0\hat{e}_y $ , $ v_0 >0 $ 且为常数,导体圆环开始绕 $ x $ 轴转动.求施加的该瞬时冲量的大小. (10分)
- 在(4)的条件下,试推导导体圆环中的电流的大小和方向与 $ \theta $ 的关系式. (10分)
- 在(4)的条件下,分析导体圆环的转动方向是否会发生改变,若是,请说明会在什么位置改变,若否,请 计算导体圆环绕 $ x $ 轴转动的角速度的最小值. 进一步地,假设 $ v_0 $ 非常小,试求导体圆环运动的最小正周期. (11分)
- 考虑经典的核子-电子体系.若原子核的原子序数为 $ Z $ ,已知绕核旋转的电子质量为 $ m $ ,元电荷为 $ e $ ,静电常数为 $ k $ ,光速为 $ c $ ,普朗克常数为 $ h $ . 忽略原子核的运动和体积.
- 忽略相对论效应,试求电子绕核做圆周运动的动能与轨道半径的关系. (4分)
- 当原子序数相当大且电子很靠近原子核时,相对论效应引起的电子质量变化往往不可忽略,考虑到此效应后,试求电子绕核做圆周运动的动能与轨道半径的关系. (8分)
- 在经典力学中,稳定存在的原子是难以理解的,因为运动电荷总是不断地辐射出电磁波进而失去能量坠落进原子核中. 为了解释这个困难,在1913年, 玻尔提出了他的玻尔模型:
· 电子围绕原子核做圆周运动.
· 电子只能处在一系列定态轨道上.
· 电子的定态轨道周长是它的德布罗意波长 $ (\lambda=h/p) $ 的正整数倍.
在(2)的条件下,试求电子最低能级的定态轨道的半径和能量,并求出非相对论极限的表达式. (11分) - 相对论力学要求任何实物粒子的运动速度不超过光速,试从此出发给出原子序数 $ Z $ 的理论上限. (11分)
- 事实上,对于较大的 $ Z $ 值,原子核的体积不再能忽略,理论表明,当假设电荷均匀发布在核半径 $ r_0 $ 时内部时,相对论性电子基态能级可以达到负值,且 $ r_0 $ 确定, $ Z $ 越大,基态能量 $ E_1 $ 越小.当 $ Z $ 达到某一 上限时,连“裸原子核”也不会稳定存在,这是因为此时核周围的电场如此之强,使得可以自发产生正负电子对,正电子飞向无穷远,电子落入核内发生逆 $ \beta $ 衰变减小 $ Z $ 值.试求基态能量低到何值时原子核会不稳定. (16分)
- 已知介质的声速可以通过以下公式计算出来:\[c=\sqrt{\left(\frac{\partial p}{\partial \rho}\right)_s}\]根号下的偏导数的意义是,在绝热条件(熵不变)求压强对气体密度的导数.(其它热力学量应化作为密度和熵为变量的函数)
- 试求摩尔质量为 $ M $ 的单原子理想气体温度为 $ T $ 时的声速. (3分)
- 试求摩尔质量为 $ M $ 的单原子范德瓦尔斯气体温度为 $ T $ 时的声速. (11分)
- 摩尔质量为 $ M $ 的单原子理想气体中分散有该种气体的小液滴(液滴质量远小于气体质量),该液滴 对应液体的密度为 $ \rho $ ,已知气体与液滴处于平衡态,压强为 $ p $ ,温度为 $ T $ ,该压强下的单位质量液体汽化潜热为 $ q $ ,求此种介质中的声速. (16分)
- 假设某容器中充满 $ N $ 个摩尔质量为 $ M $ 的单原子理想气体,若该理想气体与容器中的热辐射(光子气体)达到温度为 $ T $ 的热平衡,且 $ T $ 很高,以至于热辐射本身的压强与理想气体的压强一样大,试求容器中的声速. (20分)
第七届OPhO决赛参考答案
-
- \[d=\left|\frac{2m+1}{n_1-n_2}\right|\frac{\lambda}{4} ,\qquad m\in \mathbb{Z}\]
- \[\phi_2=\frac{1}{4}\left(\pi n+2\phi_1\right) ,\qquad n\in \mathbb{Z}\]当 $ n $ 取偶数是光 强极大值点,取奇数时是光强极小值点,光强分别为:\[E^2\left[\cos ^2 \phi_1+\sin^2 \phi_1 \sin ^2 \frac{\delta}{2}\right]\]\[E^2\cos ^2 \phi_1\left(1-\sin ^2 \frac{\delta}{2}\right)\]
- \[\delta=2 \pi \frac{d}{\lambda}\left[{\sqrt{n_2^2-\sin^2\theta}}-{\sqrt{n_1^2-\sin^2\theta}}\right]\]
- 以题图中A点为原点,光轴为 $ z $ 轴建立平面直角坐标系,等相位面方程为:\[(x^2+y^2)^2=c^2(x^2+y^2+z^2)\]$ c $ 为常数.
-
- \[T\in \left[0,\left(\frac{L-\pi r}{2}+r\right)\lambda g\right]\]
- 所需用时为:\[t=\sqrt{\frac{L}{2 g}}\ln\left(\frac{2L}{x}\right)\]平均支持力为:\[\overline{N}_{x}=2\lambda g r\ln\left(\frac{x}{2L}\right)\]\[\overline{N}_{y}=\pi\lambda g r\ln\left(\frac{x}{2L}\right)\]
- 所需用时为:\[t=\sqrt{\frac{L}{2 g}}\ln\left(\frac{2L-2\pi r}{x}\right)\]平均支持力为:\[\overline{N}_{x}=2\lambda g r\ln\left(\frac{x}{2L-2\pi r}\right)\]\[\overline{N}_{y}=\pi\lambda g r\ln\left(\frac{x}{2L-2\pi r}\right)\]
- \[\Delta x=2\left(\frac{\mu+\mu^2}{1+\mu^2}\right)r+\left(L-\pi r\right)\tanh\left(\frac{\mu \pi}{2}\right)\]
-
- \[\varPhi_0=0 \]\[\varPhi_{{\pi}/{2}}=\pi B_0 r^2 \]
- \[\varPhi=\pi B_0 r^2 \sin\theta \]导体圆环内产生感生电流需要 $ 0 < \theta < \pi $ ;若 $ B_0 $ 随时间增大,感生电流的右手螺旋方向和 $ \vec{n} $ 相反;若 $ B_0 $ 随时间减小,感生电流的右手螺旋方向和 $ \vec{n} $ 相同, $ \boldsymbol{n} $ 的方向为尽可能沿 $ z $ 轴的圆环平面法向量
- \[Q=\frac{\pi^2 r^4 k^2}{R}\left[t+\frac{2L}{R}\exp\left(-\frac{R}{L}t\right)-\frac{L}{2R}\exp\left(-\frac{2R}{L}\right)\right]\]
- 瞬时冲量大小为:\[\frac{mv_0}{2}\]
- \[I=-\frac{\pi B_0 r^2 \sin\theta}{L} \]正负分别对应电流的右手螺旋方向与 $ \vec{n} $ 相同和 相反, $ \boldsymbol{n} $ 的方向为尽可能沿 $ z $ 轴正方向的圆环平面法向量
- 否.\\\[\omega_{\text{min}}=\sqrt{\frac{v_0^2}{r^2}-\frac{2\pi^2 B_0^2 r^2}{mL}} \]\[T=\frac{\sqrt{2mL}}{B_0 r} \]
-
- \[E_k=\frac{k Z e^2}{2 r}\]
- \[E_k=\left(\sqrt{\frac{2}{2+x-\sqrt{x^2+4x}}}-1\right) mc^2 ,\qquad x=\frac{k^2 Z^2 e^4}{m^2 r^2 c^4}\]
- 基态轨道半径:\[r_1=\frac{ \hbar^2}{m k Z e^2} \sqrt{1-\left(\frac{k Z e^2}{\hbar c}\right)^2}\]非相对论极限:\[r_1=\frac{ \hbar^2}{m k Z e^2}\]基态能量:\[E_1=m c^2 \sqrt{1-\frac{k^2Z^2 e^4}{\hbar^2c^2}}\]非相对论极限:\[E_1=-\frac{m Z^2}{2}\left(\frac{k e^2 } {\hbar}\right)^2\]
- \[Z\leqslant 137\]
- \[E_{1\text{min}}=-mc^2\]
-
- \[\sqrt{\frac{5RT}{3M}}\]
- \[\sqrt{\frac{5MRT}{3(M-\rho b)^2}-\frac{2\rho a}{M^2}}\]
- \[\left[\frac{M}{RT}-\frac{2}{q}+\frac{5RT}{2Mq^2}\right]^{-1/2}\]
- \[\sqrt{\frac{77 RT}{27 M}}\]