线上物理竞赛 Online Physics Olympiad

第六届OPhO预赛试题

解答题：从下列六道选题中任选四道作答，每道题25分，多做的部分不给分

1. 如图所示是陆末—格尔克干涉仪的构造图，其由一块平行平面玻璃板和放在其一端上的直角三棱镜构成. 光线经由棱镜的直角边进入玻璃板，然后在玻璃板内部多次反射，每次反射都会有一部分光线折射出玻璃板并被足够大的焦距为 $ f $ 的 薄凸透镜L汇聚在焦平面的屏S上呈像，并出现干涉图案. 现已知空气折射率为 $ n_1 $ ，棱镜和玻璃板的折射率为 $ n_2(n_2 >n_1) $ ，玻璃板厚度为 $ d $ . 使用的单色光源的真空波长为 $ \lambda $ .
   
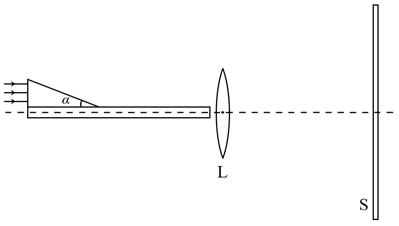
   1. 简要说明此干涉仪中凸透镜所起到的作用. (3分)
   2. 如果入射光平行于玻璃板，试求在棱镜内发生全反射并且在玻璃板内不发生全反射时，棱镜斜面与玻璃板的夹角 $ \alpha $ 所应满足的条件. (5分)
   3. 在(2)的条件下，试分别求在屏S上形成的条纹达到最亮和最暗时 $ \alpha $ 的值. (7分)
   4. 若现将点光源放在距棱镜有限距离处，此时屏S中心是暗纹，试求屏S上从中心向外数第 $ m $ 条亮纹到 中轴线的距离. (10分)
2. 如图所示，足够大的光滑水平地面上放置一个截面为直角三角形的柱形斜面体，斜面体截面的水平直角边长度为 $ L_0 $ ，斜面与地面的夹角为 $ \theta $ . 在斜面上角固定一个轻质小滑轮，球A与球B可视为质点，球B的质量为 $ M $ . 两球用一 条不可伸长的轻质细绳系住，细绳绕过滑轮且处于绷紧状态. 细绳与滑轮间的摩擦力忽略不计，重力加速度为 $ g $ ，真空光速为 $ c $ ，忽略空气阻力.
   
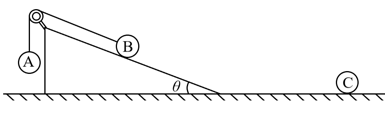
   1. 若斜面光滑，且斜面体静止时，球A和球B可以与斜面相对静止. 试求球A的质量. (2分)
   2. 若斜面体固定在地面上，球B与斜面间的动摩擦因数为 $ \mu $ ，最大静摩擦力等于动摩擦力. 如果球A 与球B能与斜面保持相对静止，试求球A质量的取值范围. (4分)
   3. 在(1)的条件下，若使斜面体在地面上沿水平方向以大小为 $ u $ 的速度运动，当 $ u $ 接近光速 $ c $ 时，试计算斜面此时的倾角. (4分)
   4. 在(3)的条件下，在运动的斜面的参考系看来，斜面速度为0，倾角仍为 $ \theta $ ，两球仍然与斜面能保持相对静止；而在地面参考系看来，斜面倾角改变，两球无法与斜面保持相对静止. 试判断两球究竟能否与斜面相对静止，并定性解释此佯谬. (5分)
   5. 在(1)的条件下，若斜面和地面均光滑，现剪断绳子，使球B下滑到地面上获得速度大小 $ v_1 $ ，同时 给地面上质量为 $ m^\prime $ 的球C施加初速度 $ v_2(v_2< v_1) $ ，两球速度同向. 之后两球发生对心完全弹性碰撞，若每次碰撞后都立即使两球速度同时反向，但保持速度大小不变，从而两球会再次碰撞. 如此反复操作，试求第 $ N $ 次使两球速度反向后的瞬间两 球的速度. 忽略相对论效应. (10分)
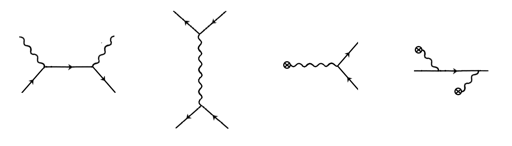
3. 在量子电动力学中，一种观点是可以用费曼图表示微观物理过程. 我们约定，在费曼图中由左至右是时间演化的方向，带箭头的直线代表电子或正电子，箭头指向是电子运动的方向或正电子运动的反方向；波浪线代表光子. 费曼图中最外的线代表实粒子，而内部的线代表虚粒子.
   
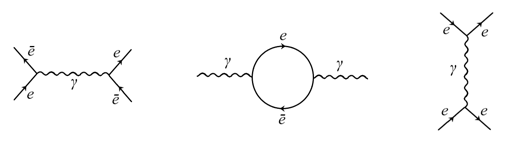
   例如 ，上图的左侧图表示的过程是一个电子 $ e $ 与一个正电子 $ \bar{e} $ 湮没为虚光子 $ \gamma $ ，再转化回一对正负电子；中间图表示一个实光子 $ \gamma $ 转化为一对虚正负电子 $ e\bar{e} $ ，再经历湮没回到一个实光子；右侧图表示两个电子 $ e $ 碰撞（散 射）并交换了一个虚光子 $ \gamma $ . 费曼图所描述的微观物理过程始终遵循动量守恒和能量守恒，粒子的能量与动量需用相对论公式计算. 普朗克常数 $ h $ 、真空光速 $ c $ 及正负电子质量 $ m $ 已知.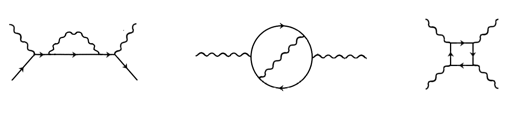
   
   1. 试描述上图所示的三幅费曼图所表示的物理过程. (5分)
      
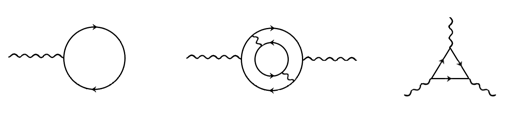
   2. 试判断上图的三幅图在现实中能否发生，并阐述理由. (6分)
   3. 画出以下物理过程的费曼图.
      (i) 康普顿散射：一个电子与一个光子碰撞
      (ii) 莫特散射：两个正电子碰撞
      (iii) 光子衰变：在电磁场中的一个光子变成一对正负电子
      (iv) 一个电子在匀强电场中加速
      *注意：费曼图中，外电磁场可以用一些“ $ \otimes $ ”符号发出的虚光子线表示. (7分)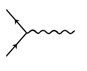
      
   4. 上图的费曼图可以表示一个自由电子辐射一个光子. 试从能量及动量守恒的角度证明自由电子辐射光子的不可能性. (7分)
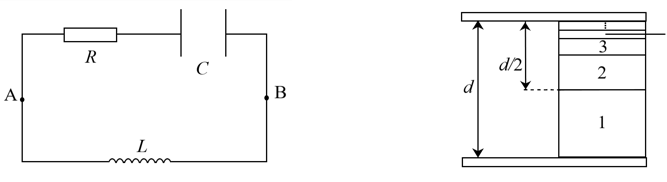
4. 考虑如图左图所示的电路，已知定值电阻的阻值为 $ R $ ，平行板电容器的电容为 $ C $ ，板间距为 $ d $ ， 电感器的电感为 $ L $ ，真空电容率为 $ \varepsilon_{0} $ .
   
   1. 若电路中没有电阻，即 $ R=0 $ 时，电路的电流与电压随时间可能形成正弦函数式的振荡，这种振荡电 路与弹簧振子的简谐振动间可以建立对应关系. 简述这种振荡形成的原因，并填写下表的空缺. (6分)

      弹簧振子		$LC$ 振荡电路
      名称	符号或表达式	名称	符号或表达式
      振子的位置	$x$
      振子的速度	$v$
      振子受到的合力	$F$
      振子的质量	$m$
      弹簧的劲度系数	$k$
      振子的动能	$E_k=mv^2/2$
      系统的势能
      震动周期		振荡周期	$T=2\pi\sqrt{LC}$

   2. 图右图为左图电路中的电容器截面图，左侧的 $ {1}/{\beta} $ 是真空，右侧剩余部分填充着由不同电 容率的材料堆叠而成的电介质，从下向上数第 $ i $ 层材料的厚度为 $ d/2^i $ ，电容率为 $ \varepsilon_{i}=\varepsilon\lambda^{i-1} $ ， $ \lambda(\lambda >1) $ 及 $ \varepsilon $ 为已知常数. 并且已知第一层材料底部极化电荷面密度为 $ \sigma_0 $ ，试求电容器正对面积及第 $ i $ 层材料顶部的极化电荷面密度. 忽略边缘效应. (9分)
   3. 若在图左图电路中A与B两点间并联一个频率为 $ f $ 的简谐交流电源，试求此电路的阻抗及干路电流与 电压间的相位差. (10分)
5. 如图所示是一系列同圆心的在同一竖直平面内的圆弧管道，它们的开口同在一条水平直线上. 管口所在直线到圆心的垂直距离为 $ h $ ，最内侧管道的圆弧的半径为 $ R_1 $ . 重力常数为 $ g $ ，忽略空气阻力. 小球可以在管内无摩擦阻力地滑行 ，小球碰到管道内壁时没有动能损失.
   
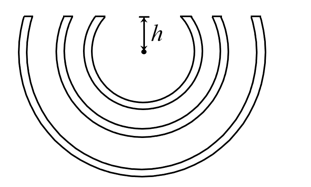
   1. 在最内侧管道的管口处向管内以初速度 $ v_0 $ 丢入一个小球，若小球从管口再次射出时恰好可以掉入 从内侧数第二个管道，试求第二个管道的弧半径. (4分)
   2. 若在最内侧的管口以初速度 $ v_0 $ 丢入小球，小球从另一侧管口射出后，刚好掉进第二个管道，再射 出后掉进第三个管道，依此类推. 试求通过此种方法小球掉入的最外层管道的弧半径. (6分)
   3. 若以某一初速度向内侧第一个管内丢入的小球可以以某一路径交替循环地在最内侧三个管道内滑行，试给出一种可能的路径的 $ R_2 $ 和 $ R_3 $ ，并指出一种无论 $ R_2 $ 和 $ R_3 $ 取何值都不可能的路径，并说明不可能的理由. (7分)
   4. 若在往外数第 $ n $ 个弧半径为 $ R_n $ 的管道的管口以初速度 $ v $ 丢入小球，小球从另一侧管口 射出后，刚好可以掉进第 $ n-1 $ 个管道同侧的管口中，再从另一侧管口射出，掉入同侧第 $ n-2 $ 个管道，依此类推，最后掉入最内侧的管道. 试证明此过程中小球在管道外空中的飞行时间大于 $ R_1(R_n-R_1)/v_0h $ . (8分)
6. 热力学第二定律指出，任何通过从热源吸热而转化为机械功的过程都具有一个转化的上限. 存在这个上限是因为转化的过程会使系统的熵增大或至多是熵保持不变. 当体系的总熵保持不变时，可以从热源中获得最大的机械功. 已知物质的量为 $ n $ ，定压摩尔热容为 $ c $ 的理想气体的熵可以用如下公式来计算： \[S=nc\ln T+nc-nR\ln p+S_0\] 其中 $ R $ 是气体 普适常数， $ S_0 $ 是只与气体种类有关的常数. 现考虑有两个绝热气体容器. 气体普适常数 $ R $ 及玻尔兹曼常数 $ k $ 已知.
   1. 说明 $ \ln T $ 及 $ \ln p $ 的单位是什么，并解释题给的熵公式中有量纲的物理量 $ T $ 或 $ p $ 取单位不同时，熵的计算结果是否一致，并说明一致或不一致的原因. (3分)
   2. 对于两种单个分子所含原子数相同的理想气体，判断它们的 $ S_0 $ 是否相同，并简述原因. (4分)
   3. 现在其中一个体积固定的绝热密闭容器中充入分子数为 $ N $ ，温度为 $ T $ 的单原子理想气体. 若外界压强恒定，温度恒为 $ T_0(T_0< T) $ . 现在冷却容器内的气体到与外界相同温度，过程足够缓慢故容器内气体可以时刻视为平衡态. 试求可以从这个过程中获得的最大机械功. (8分)
   4. 现在其中一个体积可变的绝热密闭容器中充入分子数为 $ N $ ，温度为 $ T $ ，压强为 $ p $ 的单原 子理想气体，外界的温度为 $ T_0(T_0< T) $ ，外界压强恒为 $ p_0(p_0< p) $ . 现冷却容器内的气体到与外界相同，且压强也达到与外界相同，过程足够缓慢故容器内气体可以时刻视为平衡态. 试求可以从此过程获得的最大机械功. (10分)

第六届OPhO预赛参考答案

1. 1. 使光平行光汇聚在屏S上成像，在像点发生干涉.
   2. \[\frac{1}{2} \arccos \frac{n_1}{n_2}< \alpha< \arccos \frac{n_1}{n_2}\]
   3. 干涉条纹最亮时：\[\alpha=\frac{1}{2} \arcsin \left[\frac{k \lambda}{2 n_2 d}\right]~,\qquad k\in \mathbb{N}\]干涉条纹最暗时：\[\alpha=\frac{1}{2} \arcsin \left[\frac{(2 k-1) \lambda}{4 n_2 d}\right]~,\qquad k\in \mathbb{N}\]
   4. \[ f \sqrt{\frac{8(2 m-1) d \sqrt{n_2^2-n_1^2}+(2 m-1)^2 \lambda}{8(1-2 m) d \sqrt{n_2^2-n_1^2}-(2 m-1)^2 \lambda+16 n_1^2 d^2}} \]
2. 1. \[M\sin\theta\]
   2. 球A质量 $ m $ 取值范围需分类讨论. 当：\[\mu\geqslant \tan\theta\]时：\[0< m\leqslant M(\sin\theta+\mu\cos\theta)\]当：\[0< \mu< \tan\theta\]时：\[M(\sin \theta-\mu \cos \theta) \leqslant m \leqslant M(\sin \theta+\mu \cos \theta)\]
   3. \[\lim_{u\rightarrow c}\theta\rightarrow \frac{\pi}{2}\]
   4. 可以相对静止. 理由：力学规律不应随参考系的改变而改变. 从斜面系变换到地面系，力应该使用四维力矢量进行变换后得到，这样得到的地面系的力也同样满足平衡条件.
   5. 第 $ N $ 次碰撞后瞬间两球的速度：\[v_B=\frac{\left[(-1)^N M+m^{\prime}\right] v_1+\left[(-1)^N-1\right] m^{\prime} v_2}{M+m^{\prime}} \]\[ v_C=\frac{\left[(-1)^N-1\right] M v_1+\left[(-1)^N m^{\prime}+M\right] v_2}{M+m^{\prime}}\]
3. 1. 左侧图表示一个电子吸收一个光子，然后发射一个虚光子后再吸收之，最后发射一个光子；中间图表示一个光子衰变为一对虚正负电子，虚正电子发射一个虚光子被虚电子吸收，虚电子对再湮没回一个光子；右侧图表示两个实光子交换虚的电子与正电子再出射.
   2. 左侧图的光子凭空消失，能动量不守恒，不可能发生；中间图可以发生；右侧图中下方电子线的方向反了，这种费曼图不符合规则，不可能发生.
   3. 
      
   4. 略
4. 1. 水平面上的无阻尼弹簧振子的运动方程与振荡电路的电容上的电荷 $ Q $ 所满足的微分方程相似，因此弹簧振子和LC振荡电路可以进行类比.

      弹簧振子		$LC$ 振荡电路
      名称	符号或表达式	名称	符号或表达式
      振子的位置	$x$	电容器所带电荷量	$Q$
      振子的速度	$v$	流过电感器的电流	$I$
      振子受到的合力	$F$	$A$ 、 $B$ 两点间的电势差	$U$
      振子的质量	$m$	电感	$L$
      弹簧的劲度系数	$k$	电容的倒数	$1/C$
      振子的动能	$E_k=mv^2/2$	电感器的储能	$E_L=LI^2/2$
      系统的势能	$E_p=kx^2/2$	电容器的储能	$E_C=Q^2/2C$
      震动周期	$T=2\pi\sqrt{m/k}$	振荡周期	$T=2\pi\sqrt{LC}$

   2. \[S=\frac{\beta(2 \lambda-1) d C}{\left[(2 \lambda-1) \varepsilon_0+(\beta-1) \lambda \varepsilon\right] \varepsilon_0}\]\[\sigma_i=\left(\frac{1}{\lambda^{i-1}}-\frac{1}{\lambda^i}\right) \frac{\varepsilon_0}{\varepsilon-\varepsilon_0} \sigma_0\]
   3. \[ Z=\omega L \sqrt{\frac{1+\omega^2 C^2 R^2}{(\omega C R)^2+\left(1-\omega^2 L C\right)^2}} \]\[\varphi=\arctan \left[\frac{\omega^2 C^2 R^2+1-\omega^2 L C}{\omega^3 L C^2 R}\right]\]
5. 1. \[\sqrt{\left(R_1^2-h^2\right)\left(\frac{2 v_0^2 h}{g R_1^2}-1\right)^2+h^2}\]
   2. \[\sqrt{\left(\frac{v_0^2}{g}-h\right)^2+h^2}\]
   3. 记题图中的6个管口从左至右分别为1,2,3,4,5,6. 不妨设小球从3口进入最内侧管道，则可能的循环路径 为：\[\text{a.}\qquad 3\rightarrow 4\rightarrow 1\rightarrow6\rightarrow5\rightarrow2\rightarrow3\]\[\text{b.}\qquad 3\rightarrow 4\rightarrow 1\rightarrow6\rightarrow5\rightarrow2\rightarrow4\rightarrow 3 \rightarrow 6\rightarrow 1\rightarrow 2\rightarrow 5\rightarrow 3\]\[\text{c.}\qquad 3\rightarrow 4\rightarrow 1\rightarrow6\rightarrow2\rightarrow5\rightarrow4\rightarrow 3 \rightarrow 6\rightarrow 1\rightarrow 5\rightarrow 2\rightarrow 3\]\[\text{d.}\qquad 3\rightarrow 4\rightarrow 1\rightarrow6\rightarrow2\rightarrow5\rightarrow3\]\[\text{e.}\qquad 3\rightarrow 4\rightarrow 2\rightarrow5\rightarrow1\rightarrow6\rightarrow3\]\[\text{f.}\qquad 3\rightarrow 4\rightarrow 2\rightarrow5\rightarrow1\rightarrow6\rightarrow4\rightarrow 3\rightarrow5\rightarrow2\rightarrow6\rightarrow1\rightarrow3\]其中c,d路径不可能，其余路径可能. 证明略.
   4. 略
6. 1. 不能单独谈论 $ \ln T $ 或 $ \ln p $ 的单位. 熵公式中 $ S_0 $ 包含类似 $ \ln T_0 $ 及 $ \ln p_0 $ 的项，这样与公式中的 $ \ln T $ 或 $ \ln p $ 结合在一起，例如， $ \ln (p/p_0) $ 是无量纲的.
   2. 不同. 理想气体是一种理想模型，真实气体只在一定的条件下才可以看作理想气体. 对含原子数相同的理想气体，熵是依赖于气体种类的，实际上，如果选取低温高压的 $ p_0 $ 及 $ T_0 $ ，气体一定会凝聚而不能看作理想气体，这时对相同温度与压强的不同气体，其凝聚性质不同，熵一定是不同的，因此 $ S_0 $ 也不同.
   3. \[W_{\max}= \frac{3}{2} N k T_0 \ln \left(\frac{T_0}{T}\right)-\frac{3}{2} N k\left(T_0-T\right)\]
   4. \[W_{\max} =\frac{5}{2} N K T_0 \ln \left(\frac{T_0}{T}\right)-N k \ln \left(\frac{p_0}{p}\right)-N k T_0+\frac{N k T p_0}{p} -\frac{3}{2} R\left(T_0-T\right)\]

第六届OPhO决赛试题

解答题：从下列六道选题中任选四道作答，每道题25分，多做的部分不给分

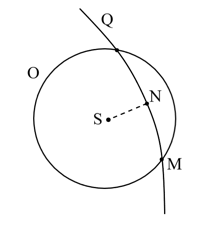
1. 考虑一颗质量为 $ m $ 的行星绕中心的质量为 $ M $ 的恒星S在圆轨道O上做圆周运动，如图所示，行星轨道半径为 $ R $ . Q是一支以S为焦点的双曲轨道，其近日点N到S的距离为 $ r $ ，其与轨道O相交于点M，SM与SN的夹角为 $ \alpha $ . 牛顿引力常数 $ G $ 已知，忽略相对论效应.
   
   1. 试求轨道O上行星的动能与引力势能. (2分)
   2. 若轨道Q上有一颗质量为 $ m $ 的彗星，试求该彗星在离恒星S无限远处的动能. (4分)
   3. 若欲使轨道O上的行星到达M时将一颗质量为 $ m_0(m_0\ll m) $ 的卫星发射进Q轨道，试求发射的卫星相对行星的速度大小. (9分)
   4. 在(3)的条件下，若考虑恒星S在围绕银河系中心质量为 $ M_0 $ 的超巨天体做轨道半径为 $ R_0 $ 的圆周运动，且恒星S的速度方向正是由S指向N. 试求质量为 $ m_0 $ 的该卫星脱离恒星S后在围绕银河系中心超巨天体做椭圆轨道运动的周 期. (10分)
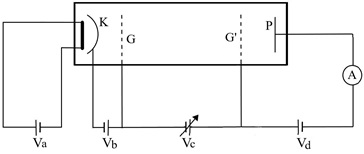
2. 如图所示为改良弗兰克—赫兹实验装置图. 在四极管中充入稀薄气体，电源Va给灯丝加热致使阴极K发射电 子，电子在KG区域被Vb加速到达栅极G，然后在GG $ ^\prime $ 区域被Vc加速到达栅极G $ ^\prime $ ，同时与气体原子碰撞. 此时，如果电子剩余足够多能量，则可以克服反向电压Vd而到达阳极P，使电流计A上出现示数. KG和G $ ^\prime $ P区域远窄于GG $ ^\prime $ ，故可忽略电子在这两个区域与原子的碰撞. 现在四极管中充入稀薄氦气，加热使阴极K发射电子，电子的发射初速度可视为0. 缓慢增大Vc的电压，发现当Vc的电压为 $ U_{1} $ 时，电流表示数出现首个极大值. 最终的电流表A示数会随Vc电压的增大出现等间距的极值. 已知Vb和Vd两端电压分别为 $ U_b $ 和 $ U_d $ ，电子质量为 $ m_e $ . 氦原子质量为 $ M(m_e\ll M) $ 且可近似视为静止的. 元电荷为 $ e $ . 忽略相对论效应.
   
   1. 此实验氦气密度既不能过高也不能过低，简述其原因. (2分)
   2. 试求氦原子的第一激发能. (3分)
   3. 试求电流表示数达到第 $ n $ 个极大值及第 $ n $ 个极小值所对应Vc的电压. (5分)
   4. 若一个电子一共激发了 $ N $ 个氦原子，并且能够到达阳极P，试求其到达P时剩余动能的取值范围. (5 分)
   5. 若阴极K由 $ {\mu} $ 子原子制成， $ \mu $ 子质量为 $ m_\mu $ ，在非相对论情形其与电子的唯一区别是其质量与氦原子的 $ M $ 相比并不可忽略. 试计算此时电流计示数首个极大值和极小值对应Vc的电压. (10分)
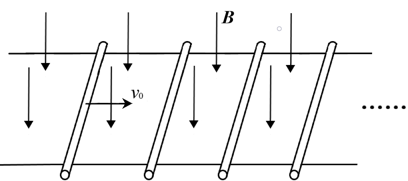
3. 如图所示，水平面上的光滑的平行直导轨间距为 $ l $ ，其上横有 $ N(N\geqslant 1) $ 根静止的导体棒，每根导体棒的质量均为 $ m $ ，电阻均为 $ R $ ，现在施加垂直于导轨平面向下的磁感应强度大小为 $ B $ 的匀强磁场. 导轨的电阻忽略 不计. 现在给第一根导体棒一个向右的水平初速度 $ v_0 $ . 假设导体棒的间距足够大而彼此间不会发生碰撞.
   
   1. 若 $ N=1 $ ，试判断导体棒内部的动生电动势的方向. (1分)
   2. 若 $ N=2 $ ，试求最终通过两根导体棒内部的电荷量. (4分)
   3. 若 $ N=3 $ ，试求最终任意的两根导体棒的位移之差. (6分)
   4. 若 $ N=4 $ ，试求最终在每根导体棒上产生的焦耳热. (6分)
   5. 对任意的 $ N $ ，试求第 $ i(i\leqslant N) $ 根导体棒的位移、速度以及通过其内部的电荷量与时间 $ t $ 的关系式. (8分)
4. 在固液气三种物态的交界线上，存在着细致的张力平衡. 表面张力系数依赖于该界面两侧的物态，并使界面有收缩的趋势. 在本题中，已知A种气体与B种固体间、A种气体与C种液体间、B种固体与C种液体间的表面张力系数分别 $ \alpha, \beta, \gamma $ . 固体B和液体C的密度分别为 $ \rho_1 $ 和 $ \rho_2 $ ，均不可压缩. 忽略液体和固体的热膨胀及热传导，表面张力不可忽略. 气体A可以视为理想气体，外界的气体A的压强恒为 $ p_0 $ . 重力加速度为 $ g $ .
   1. 简要阐述表面张力形成的原因. (1分)
      
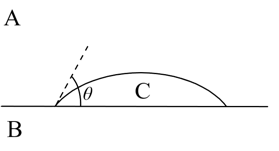
   2. 如上所示是液滴C在气体A中附着在固体B的表面的截面图. 试求气体A中的液滴C在固体B表面的接触角 $ \theta $ . (3分)
      
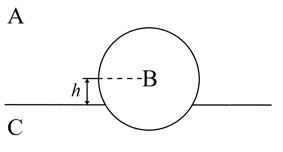
   3. 如上图所示，将由固体B制成的半径为 $ r $ 的实心小球浸入液体C中，试求平衡时小球的球心距离C的液体表面的高度 $ h $ （列出方程即可）. (10分)
      
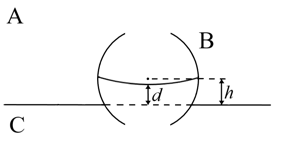
   4. 如上图所示，将由固体B制成的半径为 $ r $ 的薄壁球壳上下开口浸入液体C，外界连通气体A，平衡时薄壁球壳的球心在球外C的液面正上方 $ h $ 处. 试求球壳内部液面上升的高度 $ d $ （列出方程即可），并求曲率半径 $ \rho $ 与 $ d $ 的关系式. (11分)
5. 如图所示是一系列共轴排列的两个球形折射面（图中分别标记为1,2），从左数起的第 $ i(i\leqslant 2) $ 个折射面的半径为 $ r_i $ ，第 $ i $ 个折射面的球心与 $ i+1 $ 个折射面的球心的距离为 $ d_i $ . 第一个折射面左侧空气的折射率为 $ n_0 $ ，第 $ i $ 个折射面到第 $ i+1 $ 个折射面之间部分的折射率为 $ n_i $ ，两个折射面的球心均在折射面右侧. 现有一条与光轴夹角为 $ \theta $ 的光射向第一个折射面，入射点P到光轴的垂直距离为 $ y_0 $ . 假设光线会过所有的折射面并发生折射，不考虑发生全反射的情况. 折射面均不为平面.
   
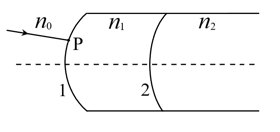
   1. 写出光线与光轴相交次数的取值范围. (2分)
   2. 若入射光与光轴平行，且光线在第二个折射面右侧第一次与光轴相交，试求此交点到第一个折射面球心的距离. (8分)
   3. 试求从第二个折射面出射的光线与光轴的夹角. (15分)
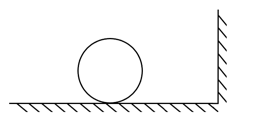
6. 如图所示，水平地面上放置放置一个质量为 $ m $ 的圆柱体，圆柱体的半径为 $ R $ ，初始时刻圆柱体截面的圆心距离右侧竖直墙的距离为 $ L $ . 现在给圆柱一个无平动的转动初角速度 $ \omega_0 $ . 已知圆柱与竖直墙壁间的碰撞是完全弹性 的，且碰撞时间极短，碰撞时只改变圆柱质心速度，不改变其转动角速度. 地面与圆柱间的滑动摩擦系数为 $ \mu $ ，忽略圆柱与地面 间的滚动摩阻（即纯滚动时无摩擦力与阻力矩）. 重力加速度为 $ g $ .
   
   1. 试求该圆柱刚开始转动时的动能. (2分)
   2. 若圆柱刚开始的转动是逆时针的，试求最终圆柱质心的速度及摩擦产生的热量. (8分)
   3. 若圆柱刚开始的转动是顺时针的，试求最终圆柱质心的速度及摩擦产生的热量. (15分)

第六届OPhO决赛参考答案

1. 1. \[E_p=-\frac{GMm}{R}\]\[E_k=\frac{GMm}{2R}\]
   2. \[E=\frac{G M m_0}{2r}\left(\frac{R-R\cos\alpha}{r-R \cos \alpha}\right)\]
   3. 相对速度大小为：\[\sqrt{\frac{G M}{r}\left(\frac{r-R}{R \cos \alpha-r}-1\right)+\frac{G M}{R}\left[3-2 \sqrt{\frac{r}{R}\left(1+\frac{r-R}{R \cos \alpha-r}\right)}\right]}\]或\[\sqrt{\frac{G M}{r}\left(\frac{r-R}{R \cos \alpha-r}-1\right)+\frac{G M}{R}\left[3+2 \sqrt{\frac{r}{R}\left(1+\frac{r-R}{R \cos \alpha-r}\right)}\right]}\]
   4. \[ T=\frac{M_0 \pi}{\sqrt{2G}}\left[\frac{M_0}{2 R_0}-\frac{M}{2 r}\left(\frac{r-R}{R \cos \alpha-r}-1\right)-\frac{R \cos \alpha-r}{r-R} \sqrt{\frac{M_0 M}{R_0 r}\left(\frac{r-R}{R \cos \alpha-r}-1\right)}\right]^{-3 / 2} \]
2. 1. 如果氦气密度过高，会使电子平均自由程很小，导致碰撞（散射）引起的阻力系数过大，无法越过气体区. 氦气密度过低会导致电子碰到氦原子的概率过小，很难形成所需要的实验曲线.
   2. \[E_1=e\left(U_1+U_b\right)\]
   3. \[U_{\max}^{(n)}=n U_1+(n-1) U_b\]\[U_{\min }^{(n)}=e U_d+n U_1+(n-1) U_b\]
   4. 电子剩余动能取值范围为：\[E_{\text {rem }} \in\left[0, e\left(U_1+U_b-U_d\right)\right]\]
   5. 首个极大值的Vc电压为：\[\frac{m_\mu+M}{M} U_1+\frac{m_\mu}{M} U_b\]首个极小值的Vc电压为：\[\frac{M+2 m_\mu}{M+m_\mu} U_1+\frac{m_\mu}{M+m_\mu}U_b+U_d\]
3. 1. 电动势方向为由题图中的下方指向上方.
   2. \[q=\frac{mv_0}{2Bl} \]
   3. 第一根棒与第二根或第三根棒间位移差为：\[\frac{m R v_0}{B^2 l^2}\left(1-\mathrm{e}^{-\frac{B^2 l^2}{m R}t}\right)\]后两根棒间位移差为0.
   4. 第一根棒上产生的焦耳热为：\[Q=\frac{9}{32}mv_0^2\]其余每根棒上产生的焦耳热为：\[Q=\frac{23}{96}mv_0^2\]
   5. 对第一根棒：\[x(t)=\frac{(N-1) m v_0 R}{N B^2 l^2}+\frac{v_0 t}{N}-\frac{(N-1) m v_0 R}{N B^2 l^2} \mathrm{e}^{-\frac{B^2 l^2}{mR}t}\]\[v(t)=\frac{v_0}{N}+\frac{(N-1) v_0}{N} \mathrm{e}^{-\frac{B^2 l^2}{mR}t}\]\[q(t)=\frac{(N-1)m v_0}{N B l}\left(1-\mathrm{e}^{-\frac{B^2 l^2}{mR}t}\right)\]对第二至 $ N $ 根棒：\[x(t)=-\frac{m v_0 R}{N B^2 l^2}+\frac{v_0 t}{N}+\frac{m v_0 R}{N B^2 l^2} \mathrm{e}^{-\frac{B^2 l^2}{mR}t}\]\[v(t)=\frac{v_0}{N}\left(1-\mathrm{e}^{-\frac{B^2 l^2}{mR}t}\right)\]\[q(t)=\frac{m v_0}{N B l}\left(1-\mathrm{e}^{-\frac{B^2 l^2}{mR}t}\right)\]
4. 1. 略
   2. \[\theta=\arccos\left(\frac{\alpha-\gamma}{\beta}\right)\]
   3. $ h $ 的方程为：\[\sqrt{\left[\beta^2-\left(\alpha-\gamma\right)^2\right]\left(h^2-\frac{h^4}{r^2}\right)} +\rho_2 g\left(\frac{2 r+h}{6}\right)(r-h)^2=\frac{2}{3} \rho_1 g r^3\]
   4. $ d $ 的方程为：\[2\left(\alpha-\gamma\right)-2(h-d) \sqrt{\frac{\beta^2-\left(\alpha-\gamma\right)^2}{r^2-(h-d)^2}}=\rho_2 grd \]曲率半径为：\[\rho=\frac{2\beta}{\rho_2gd}\]
5. 1. 次数取值范围为：\[\{1, 2\}\]
   2. \[\frac{n_0 y_0}{n_2 \sin \left(\phi+\delta\right)}-\frac{n_1 d_1 \sin \phi}{n_2 \sin \left(\phi+\delta\right)}+d_1\]其中：\[\phi=\arcsin\left(\frac{y_0}{r_1}\right)-\arcsin\left(\frac{n_0y_0}{n_1r_1}\right)\]\[\delta=\arcsin\left(\frac{n_0y_0}{n_1r_2}-\frac{d_1}{r_2}\sin\phi\right)-\arcsin\left(\frac{n_0y_0}{n_2r_2}-\frac{n_1d_1}{n_2r_2}\sin\phi\right)\]
   3. \[\phi+\arcsin\left( \frac{y_0 \cot \theta-\sqrt{r_1^2-y_0^2}}{n_1r_2} n_0\sin \theta-\frac{d_1}{r_2} \sin \phi\right)-\arcsin\left( \frac{y_0 \cot \theta-\sqrt{r_1^2-y_0^2}}{n_2r_2} n_0\sin \theta-\frac{n_1d_1}{n_2r_2} \sin \phi\right)\]其中：\[\phi=\theta+\arcsin\left(\frac{y_0 \cot \theta-\sqrt{r_1^2-y_0^2}}{r_1} \sin \theta\right)-\arcsin\left(\frac{y_0 \cot \theta-\sqrt{r_1^2-y_0^2}}{n_1r_1} n_0\sin \theta\right)\]
6. 1. \[\frac{1}{4}m\omega_0^2R^2\]
   2. \[v_c=\frac{1}{3}\omega_0R\]\[Q=\frac{1}{6}m\omega_0^2R^2\]
   3. 需分情况讨论. 若：\[{\omega_0^2 R^2} \leqslant{18 \mu g}( L-R)\]则：\[v_c=\frac{1}{9}\omega_0R\]\[Q=\frac{13}{54}m\omega_0^2R^2\]若：\[18 \mu g(L-R)< \omega_0^2 R^2\leqslant32 \mu g(L-R)\]则：\[v_c=\frac{4}{3} \sqrt{\frac{2 \mu g(L-R)}{\mu g}}-\frac{\omega_0 R}{3}\]\[Q=\frac{m \omega_0^2 R^2}{6}+\frac{2 m \omega_0 R}{3} \sqrt{2 \mu g(L-R)}-\frac{8 \mu m g(L-R)}{3}\]若：\[\omega_0^2 R^2 >32 \mu g(L-R)\]则：\[v_c=\frac{1}{3} \omega_0 R-\frac{4}{3 \mu g} \sqrt{2 \mu g(L-R)}\]\[Q=\frac{2 m \omega_0^2 R^2}{3}-\frac{10 m \omega_0 R}{3} \sqrt{2 \mu g(L-R)}+\frac{40 \mu m g(L-R)}{3}\]