线上物理竞赛 Online Physics Olympiad

第五届OPhO预赛试题

一. 选做题：解答题，从下列两道选题中任选一道作答，每道题10分，多做的部分不给分

1. 如图所示是两个纯电阻电路，已知电源电压均恒为 $ U $ ，定值电阻阻值均为 $ R_0 $ ，电路中其余导线的电阻及电源内阻不计.
   
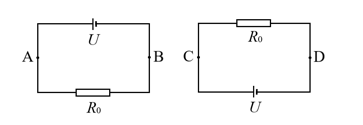
   1. 现用一根电阻恒定为 $ R $ 的铜线将两个电路中的B点和C点接通（铜线不与电路的其它部分接触），试 求此时通过两个定值电阻的电流分别是多少. (2分)
   2. 现用一根电阻恒定为 $ R $ 的铜线将两个电路中的B点和C点接通（铜线不与电路的其它部分接触），再 用一根电阻为 $ R $ 的铜线将两个电路中的A点和D点接通，试求此时通过两根铜线中的电流方向及大小. (4分)
   3. 现用一根电阻恒定为 $ R $ 的铜线将两个电路中的B点和D点接通（铜线不与电路的其它部分接触），再 用一根电阻为 $ R $ 的铜线将两个电路中的A点和C点接通，试求此时电路中的总电功率. (4分)
2. 现有两列车分别在两列平行的直轨道上同向行驶，前面的列车长 $ l_1 $ ，后面的列车长 $ l_2 $ . 在刚开始，前面的列车的车尾与后面的火车的列头对齐，且前面的列车以速度 $ v $ 匀速前进，后面的列车静止，经过时间 $ t $ 后，后面的列车以速度 $ u(u > v) $ 开始匀速前进. 只考虑声音在空气中的传播，且已知声音在空气中的传播速度恒定为 $ c(c >u) $ ，不考虑声音 随传播距离的衰减.
   1. 试求再过多久后面的列车的车尾可以超过前面的列车的车头. (2分)
   2. 如果后面列车的车头都尚未超过前面列车的车尾，如果前面列车的车头到车尾各个部位同时都发出了一声响声，前面列车发出响声时后面列车的车头尚未超过前面列车的车尾，试求后面列车的车头处的人听见这个声响持续的时间. (2分)
   3. 如果前面列车突然开始持续发出一段时间响声，假设这种响声是前面列车的车头到车尾各个部位均匀发出的，且各部分发声同时开始，同时结束. 如果后面列车的车头处的人从开始听见前面列车的声音到声音的响度达到最大值的时间为 $ T_1 $ ，且他听见响度最大的声音持续了时间 $ T_2 $ 后才开始减弱. 直到声音完全消失，后面列车的车头都尚未超过前面列车的车尾. 试求前面列车持续发出响声的时间. (6分)

二. 必做题：解答题，下面三题分别为20分、30分、40分

3. 当汽车要达到某一额定功率时，使用涡轮增压器和内燃机比只使用内燃机更节省能源. 涡轮增压器，或简称涡 轮，其工作原理如图所示，原理如下：内燃机C将排出的废气送至涡轮B，推动其转动，涡轮B再带动压气机A，压气机从大气环境D中 吸取更多气体进入内燃机C的气缸，同时增大内燃机内压，这比C直接从大气D中吸气燃烧更加充分，同时最终的废气从B排回大气. 现有一台没有涡轮增压器的质量为 $ m $ 的四冲程内燃机车，其额定功率为 $ P_0 $ ，它可以在某水平地面上以速度 $ v $ 匀速行驶. 已知 重力加速度为 $ g $ ，阻力只考虑地面摩擦力.
   
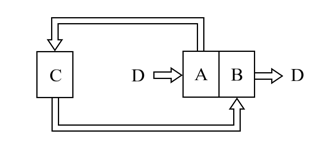
   1. 涡轮通常由可转动的机械叶片构成，试简述其工作时可以增加吸气量的原因. (2分)
   2. 试简要阐述加装涡轮增压器可以增大能源转化效率的原因. (2分)
   3. 汽车加装涡轮增压后，试判断其排气量（每次循坏气缸排出废气的质量）是增加还是减少，并简要阐述原因. (3分)
   4. 求此汽车以额定功率 $ P_0 $ 匀速行驶时受到地面的摩擦力. (3分)
   5. 现给此汽车加装一台质量为 $ M $ 的涡轮增压器，其使汽车额定功率增大至 $ P_1 $ ，试求此时汽车以 $ P_1 $ 匀速行驶时的速度. (4分)
   6. 在(5)的条件下，假设内燃机每轮循环的用时及吸入的汽油质量不变，如果想要行驶与不装涡轮增压器时 相同的路程，试求汽油量与不装时的比值至少为多少. (6分)
4. 如图所示，考虑在一足够大的薄凸透镜右侧放置一平面镜，平面镜与凸透镜的主光轴垂直. 在凸透镜左侧A点放置 一点光源. 已知若不放平面镜，且点光源到凸透镜光心的距离为 $ x $ 时，点光源将在凸透镜的右侧与凸透镜光心相距 $ nx(n >0) $ 的位置成像.
   
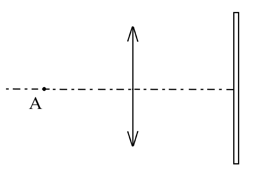
   1. 试求凸透镜的焦距. (3分)
   2. 若不放置平面镜，点光源到凸透镜光心的距离为 $ mx(m >0) $ 时，试求点光源所成像的位置与 $ x $ 的关系，并指出它们是实像还是虚像. (7分)
   3. 若放置平面镜，点光源到凸透镜光心的距离为 $ mx $ ，凸透镜到平面镜的距离也为 $ mx $ ，试求点光源所成像的个数与 $ x $ 的关系，求这些像的位置（指出在凸透镜左侧还是右侧即可），以及它们是实像还是虚像. (20分)
5. 考虑水平地面上静止放置的一个足够深的柱状容器，容器里盛放某种液体，该液体的密度 $ \rho $ 随深度 $ h $ 的变化关系恒为：\[\rho(h)=\rho_0\left(1+\frac{h}{H}\right)\]其中 $ \rho_0 $ 和 $ H $ 是已知常数。现将一个高为 $ H $ 的 实心均匀正圆柱体（正圆柱体是指底面直径等于高的圆柱体）放入该液体中，且圆柱体的底面与液体表面平行，稳定时圆柱体完全浸没在液体中. 重力加速度为 $ g $ .
   1. 试求容器中深度为 $ d $ 处的液体压强. (4分)
   2. 试分别用阿基米德原理和圆柱体上下两个底面所受到的液体压力差两种方法计算圆柱体受到的浮力大小，分析两种方法分别是否正确，并简要阐述原因. (10分)
   3. 假若现使容器和其中的液体、圆柱体整体在竖直方向上做速率均匀增大的直线运动，稳定时容器、液体、圆柱体保持相对静止，圆柱体仍浸没在液体中，假若液体的密度分布 $ ρ(h) $ 不变，试判断此时圆柱体在液体中的深度与静止情形相比是否相同，并给予证明. (10分)
   4. 考虑容器静止在地面上. 将一高度为 $ H/2 $ 的同等材质实心均匀正圆柱体放在已有正圆柱体的正上方 ，稳定后再放入高度为 $ H/4 $ 的正圆柱体，稳定后再放入高度为 $ H/8 $ 的正圆柱体……以这样的方式一直放下去，若稳定时最上面的圆柱体的深度不断接近但始终不小于 $ h_0 $ ，试求圆柱体的密度. (16分)

第五届OPhO预赛参考答案

1. 1. 电流大小均为：\[I=\frac{U}{R_0}\]
   2. 电流大小均为：\[I=\frac{U}{R}\]电流方向为 $ \rm A\rightarrow D $ ， $ \rm C\rightarrow B $ .
   3. \[P=\frac{2U^2}{R_0}\]
2. 1. \[\frac{l_1+l_2+vt}{u-v}\]
   2. \[\frac{l_1}{c+u}\]
   3. 需分情况讨论，若：\[T_1\leqslant \frac{l_1}{c+u}\]则前车发出声响时间为：\[t=\frac{c+u}{c+v}T_1\]若：\[T_1 >\frac{l_1}{c+u}\]则前车发出声响时间为：\[t=\frac{c+u}{c+v}(T_1+T_2)\]
3. 1. 因为废气可以推动涡轮旋转，涡轮的快速转动可以改变机器内外的压力差，将外界更多的气体吸入内部.
   2. 一方面，吸气量增大，可以增大内燃机的压强和气体量，首先更多的空气可以使燃料燃烧更充分，有更多的化学能被转化，另外压强大也可以使做功冲程做的功更多. 另一方面，废气的动能可以再次被加以利用，转化为更多的吸气量，从而能源利用效率更大.
   3. 增加. 由于吸入的气体量更大了，并且燃烧更充分，产生的废气也更多，因此排气量增大.
   4. \[\frac{P_0}{v}\]
   5. \[\frac{P_1 m_0}{P_0\left(m_0+M\right)} v\]
   6. \[\frac{P_0\left(m_0+M\right)}{P_1 m_0} \]
4. 1. 焦距是：\[f=\frac{n}{1+n}x\]
   2. 若：\[m< \frac{n}{1+n}\]成虚像，位置在凸透镜左侧与光心距离为：\[\frac{nm}{n-(1+n)m}x\]若：\[m >\frac{n}{1+n}\]成实像，位置在凸透镜右侧与光心距离为：\[\frac{nm}{(1+n)m-n}x\]若：\[m=\frac{n}{1+n}\]不成像.
   3. 若：\[m< \frac{n}{1+n}\]成三个像，凸透镜左侧一个虚像，右侧一个虚像，一个实像. 若：\[\frac{n}{1+n}\leqslant m< \frac{3n}{2+2n}\]成一个实像，在凸透镜左侧. 若：\[m=\frac{3n}{2+2n}\]成一个实像，在光心. 若：\[\frac{3n}{2+2n}< m< \frac{(2+\sqrt{2})n}{2+2n}\]成两个像，在凸透镜右侧一个实像，一个虚像. 若：\[m=\frac{(2+\sqrt{2})n}{2+2n}\]成一个实像，在凸透镜右侧. 若：\[\frac{(2+\sqrt{2})n}{2+2n}< m\leqslant\frac{2n}{1+n}\]成两个像，在凸透镜左侧一个实像，右侧一个实像. 若：\[m >\frac{2n}{1+n}\]成三个像，凸透镜左侧一个实像，右侧一个虚像，一个实像.
5. 1. \[p=\rho_0 g d+\frac{\rho_0 g d^2}{2 H}\]
   2. 浮力均为：\[F=\rho_0\left(\frac{3}{2}+\frac{h_1}{H}\right) \frac{\pi H^3}{4} g\]从浮力成因的角度出发来计算浮力必然正确，而阿基米德浮力原理同样适用于密度为常数的液体，故都正确.
   3. 相同. 证明略.
   4. \[\rho=\left(\frac{12}{5}+\frac{h_0}{H}\right) \rho_0\]

第五届OPhO决赛试题

一、选做题：解答题，从下列两道选题中任选一道作答，每道题25分，多做的部分不给分

1. 如图所示是一个长度为 $ L $ ，横截面积为 $ A $ 的气体容器，A、B和C是被两个无摩擦活塞隔开的三个部分， 分别都是绝热且密闭的. 两个无摩擦活塞 P 和 Q 分别被两个和一个劲度系数为 $ b $ ，原长为 $ l(2l < L) $ 的轻质弹簧相接. 现向容器的A、B 和 C三个部分中分别充入一些同种单原子理想气体，初始充入气体时弹簧处于原长. 忽略一切摩擦导致的能量损耗，活塞和 容器壁的厚度忽略不计. 已知玻尔兹曼常数为 $ k $ .
   
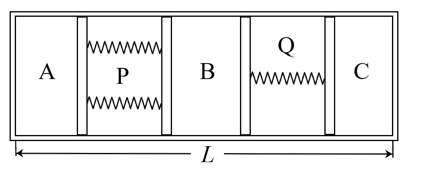
   1. 试求体系平衡时，P活塞的一个弹簧的弹性势能与Q活塞的弹簧的弹性势能之比. (2分)
   2. 若另有一个与该气体容器相类似的气体容器，其它条件完全相同，区别仅在于那一个气体容器的所有部分都是保持温度恒定的，而不是绝热的. 在两个容器中都处于平衡状态的条件下，弹簧有一个很小的偏离平衡位置的移动，试判断对于绝热和恒温两个容器，哪一个恢复平衡状态更快，并简要阐述原因. (3分)
   3. 若仅在B部分内充入某温度的单原子理想气体，试求平衡前后B部分内气体内能改变量的取值范围. (6分)
   4. 若充入容器三个部分的单原子理想气体的初始温度均为 $ T_0 $ ，体系最后达到平衡时，三个部分的温 度均为 $ T $ ，试求容器三个部分内的平衡压强. (6分)
   5. 若充入容器三个部分的气体的初始温度相等，且充入B部分的气体的量是充入A与C部分内的 $ n $ 倍. 最终平衡后，B部分的温度与初始时相同，Q活塞的弹簧长度为 $ d $ ，试求平衡后B部分的体积. (8分)
2. 在球类运动中，作自转的球体的运动轨迹往往是一条曲线，这种现象称为马格努斯效应，其成因是空气在 球体表面每一点的流速不同导致压强不同，从而产生压力差. 已知若密度为 $ \rho $ 的空气相对球体表面某一点的流速为 $ v $ ，则 其对球体该点的压强 $ p $ 可以近似用以下公式给出：\[p=p_0-\frac{1}{2}\rho v^2\]其中 $ p_0 $ 是大气压强，气体流动时的压强 $ p $ 导致的压力方向垂直于物体表面. 考虑如图所示的距地面高 $ h $ 的半径为 $ r $ ，厚度为 $ d $ 的质量为 $ m $ 的圆盘 $ (d\ll r\ll h) $ ，如果令圆盘作自由落体运动，会发现圆盘边缘上任意一点附近的空气相对于该边缘点的流速 $ V $ 与圆盘中心下落的速度 $ v $ 的关系一定满足 $ V = πv/2 $ . 现在考虑静止释放圆盘的同时令圆盘以角速度 $ \omega $ 顺时针绕圆盘的轴线转动，并 假设圆盘转动的角速度在下落过程中不变，一段时间后，圆盘落地. 忽略空气阻力，空气密度 $ \rho $ 和重力加速度 $ g $ 已知.
   
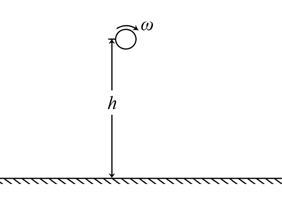
   1. 试判断圆盘会朝哪个方向移动，并简要阐述原因. (2分)
   2. 试判断圆盘“下落”过程中的竖直加速度方向是否有可能向上，并简要阐述原因. (3分)
   3. 试求圆盘落地时的速度大小. (4分)
   4. 试求圆盘落地时的水平速度大小. (7分)
   5. 试求圆盘的下落的总用时. (9分)

二、必做题：解答题，下面三题分别为15分、30分、30分

3. 光滑的水平地面上放有一个 $ N $ 足支架，其中 $ N > 2 $ 且为整数，已知支架的顶部挂有质量为 $ m $ 的负 重，支架的底部用闭合的，质量忽略不计的细绳套住，防止支架倒塌. 细绳处于绷紧的状态，支架的每个足都是长度为 $ l $ 质量可忽 略不计的硬杆. 如图所示是 $ N = 3 $ 时的 $ N $ 足支架的图例. 重力加速度为 $ g $ .
   
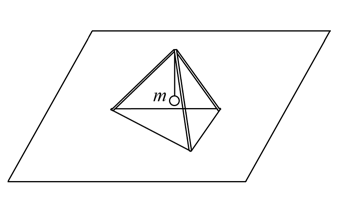
   1. 试求地面对支架的支持力大小. (1分)
   2. 试判断稳定时，底部的细绳的形状是否一定是正 $ N $ 边形，并简要阐述原因. (2分)
   3. 如果每个足与竖直方向的夹角都是 $ θ $ ，试求支架底部的细绳中的张力大小. (3分)
   4. 如果底部细绳形状为正方形时，支架的一个侧面形状恰好是等边三角形，试求此时细绳内与每根支架内的张力大小的比值. (3分)
   5. 在(4)的条件下，试分析当底面正多边形在 $ N $ 逐渐增大的过程中绳子张力的变化趋势，并确定 $ N\rightarrow{\infty} $ 时，细绳内与每根支架内的张力大小比值与 $ N $ 的近似关系式. (6分)
4. 如图所示是一种速度选择装置的剖视图，A和B是两块面积足够大的相互平行的厚度可忽略不计的圆板，两板的圆心正对，相距 $ l $ ，在A板的圆心的正上和正下各有一个可以通过粒子的孔洞，二者到圆板中心的距离均为 $ d $ . 被A隔开的左右两个区域分别记为N、M，在B板圆心处有一个可以向M区发射粒子的枪O，它可以朝各个方向发射从 $ 0 $ 到 $ v_{\mathrm{m}} $ 各个速度大小的电荷量为 $ q(q > 0) $ 的质量为 $ m $ 的带电粒子. 粒子撞在A板或 B 板孔洞以外的地方将会被吸收. 现考虑在M区施加不同方向的匀强电场，在N区施加垂直于纸面的匀强磁场. 粒子的重力忽略不计，忽略相对论效应.
   
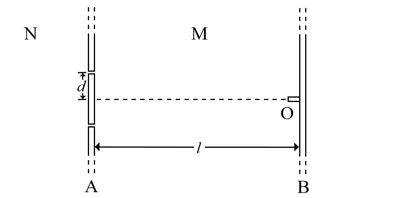
   1. 试判断带电粒子在N区运动时动能是否会改变，并简要阐述原因. (1分)
   2. 若M区的电场方向竖直向上，且枪O水平发射出速度大小为 $ v_0(v_0 < v_{\mathrm{m}}) $ 的粒子恰好 可以穿过A板上方的孔洞，若此粒子还能够再一次回到M区，试求N区的磁感应强度. (4分)
   3. 在(2)的条件下，试求该粒子从发射到被吸收的时长. (6分)
   4. 若M区的电场方向水平，且枪O发射出的粒子可以打进A板的任一孔洞，试求M区匀强度电场的电场强度的取值范围. (9分)
   5. 若M区的电场方向竖直，且枪O发射出的粒子可以打进A板正上方的孔，试求M区匀强度电场的电场强度的取值范围. (10分)
5. 宇宙中存在一种引力极强的天体，该种天体的引力强到就连光在一定的范围内也无法逃出，该种天体称为黑洞. 本题我们在理想情况下讨论黑洞的简化模型. 我们假设黑洞从外部的观测者看来，就好似一个黑色的球体，完全看不见内部的情况. 黑洞的“半径” $ R $ ，称为施瓦西半径，与黑洞的质量 $ M $ 之间的关系为：\[R=\frac{2GM}{c^2}\]而黑洞的温度 $ T $ 与其质量 $ M $ 的关系是：\[T=\frac{Kc^3}{8\pi GM}\]其中 $ G $ 是牛顿引力常数， $ c $ 是真空光速，而 $ K $ 是一个基本物理常数. 现考虑宇宙中的某个黑洞，已知其施瓦西半径为 $ R $ ，黑洞的质量和温度并未直接已知. 物理常数 $ c, G, K $ 已知. 本题仅考虑牛顿引力理论.
   1. 试求常数 $ K $ 的单位. (2分)
   2. 试求此黑洞表面的重力常加速度. (3分)
   3. 霍金指出，由于黑洞具有温度，因此黑洞存在热辐射. 如果现有一个质量为 $ m $ 的粒子从此黑洞中辐 射出去，试计算辐射粒子后黑洞的平均密度. (4分)
   4. 如果此黑洞辐射出两个粒子的时间间隔反比于辐射出前一个粒子后黑洞的温度，且此黑洞从刚开始到辐射出第一个粒子的时间为 $ \tau $ ，每次辐射的粒子质量均为 $ m $ ，试求从开始到此黑洞蒸发完所用的时间. (6分)
   5. 在(4)的条件下，试计算从刚开始到黑洞被蒸发完整个过程黑洞的平均温度. (6分)
   6. 如果此黑洞辐射出两个粒子的时间间隔反比于辐射出前面那个粒子后瞬间的黑洞表面积，且此黑洞辐射出最后的两个粒子之间的用时为 $ \tau $ ，每次辐射的粒子质量均为 $ m $ ，那么此种辐射机制的蒸发用时与(4)中的辐射机制相比哪一个更长？试证明你的结论. (9分)

第五届OPhO决赛参考答案

1. 1. \[\frac{E_p}{E_Q}=\frac{1}{4}\]
   2. 绝热时恢复平衡更快，原因是气体相同幅度的绝热压缩/绝热膨胀相比等温压缩/等温膨胀的压强变化幅度更大，因此回复力也更大.
   3. \[\Delta U\in\left[0,\frac{4}{3}b(L-l)^2\right]\]
   4. \[ p_\mathrm{A}= p_\mathrm{B}= p_\mathrm{C}=(L-2 l)\left[\frac{2 b\left(T_0-T\right)}{A\left(4 T-3 T_0\right)}\right]\]
   5. \[V_\mathrm{B}=A\left(\frac{3 L}{9+3 n}+\frac{n-1}{6+2 n} l-\frac{d}{2}\right)\]
2. 1. 圆盘会向右移动. 根据题给公式，圆盘左侧受到空气压力大于右侧受到空气压力，因此圆盘被压向右边.
   2. 可能. 因为马格努斯力具有向上的分力，而马格努斯力大小和重力大小完全没有关系，因此当 $ \omega $ 足够大时，会导致圆盘下落一段距离后向上的力将大于重力.
   3. \[\sqrt{2gh}\]
   4. \[\frac{2\pi d\rho r^2h}{m}\]
   5. \[\frac{m}{2 \pi d \rho \omega r^2} \arccos \left(1-\frac{4 \pi^2 d^2 \rho^2 \omega^2 r^4 h}{m^2 g}\right)\]
3. 1. \[G=mg\]方向竖直向上.
   2. 不一定是. 例如 $ N=3 $ 时，三条腿中的两条腿并在一起时，是一种三角形的极限情况，这种情况可能 存在.
   3. \[\frac{mg\tan\theta}{2N\sin(\pi/N)}\]
   4. \[\frac{T}{F}=\frac{1}{2}\]
   5. $ N $ 增大， $ T $ 减小.\[\lim_{N \rightarrow \infty}\frac{T}{F}\rightarrow \frac{N}{\pi^2}\]
4. 1. 不会改变. 理由：磁场导致的洛伦兹力不对带电粒子做功.
   2. \[B=\frac{mv_0}{qd}\]
   3. \[\frac{2 l}{v_0}+\frac{2 \pi d}{v_0}-\frac{2 d}{v_0} \arcsin \left(\frac{v_0}{\sqrt{v_0^2+\frac{4 v_0^2 d}{l}}}\right)\]
   4. 规定水平向左为 $ E $ 取正直的方向： \[E\in\left[-\frac{2 mv_{\mathrm{m}}^2 l}{q d^2+4 q l^2} , \frac{2 m v_{\mathrm{m}}^2 l}{q d^2}\right]\]
   5. 规定竖直向上为 $ E $ 取正直的方向：\[E\in\left[\frac{m v_{\mathrm{m}}^2\left(d-\sqrt{l^2+d^2}\right)}{q l^2} , \frac{m v_{\mathrm{m}}^2\left(d+\sqrt{l^2+d^2}\right)}{q l^2}\right]\]
5. 1. \[\mathrm{K}\cdot s\]
   2. \[\frac{c^2}{2R}\]
   3. \[\frac{3 c^6}{8 \pi G\left(R^2 c^4-4 G R m c^2+4 G^2 m^2\right)}\]
   4. \[\left(\frac{M}{2 m}+\frac{m}{M}+1\right) \tau\]
   5. \[\frac{ KM \tau}{4 \pi G M^2+8\pi G m^2+8 \pi G m M}\]
   6. 此种辐射机制的蒸发时间一定短于(4)中的辐射机制蒸发时间. 证明略.