线上物理竞赛 Online Physics Olympiad

第四届OPhO预赛试题

解答题

1. 在粗糙水平地面上固定放置一个光滑斜面，斜面顶端到地面的垂直高度为 $ h $ . 于初始 $ t = 0 $ 时刻在斜面顶端无初速度地放置一个可以视为质点的质量为 $ m $ 的物块，若于 $ t = t_1 $ 时刻物块滑落到地面上，物块于 $ t = t_2 $ 时刻 完全静止. 重力加速度为 $ g $ ，忽略一切阻力，物块从斜面上转移到地面上时速率不变.
   
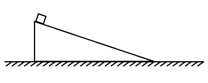
   1. 试分析物块在 $ t = 0 $ 到 $ t = t_2 $ 这个时间段内机械能是否守恒. (3分)
   2. 试求斜面对物块做的功. (3分)
   3. 试求物块与地面间的滑动摩擦系数. (4分)
   4. 试求物块在 $ t = 0 $ 到 $ t = t_2 $ 这个时间段内的路程. (5分)
2. 考虑真空中的一个粗糙的水平面上放置 $ n $ 个带电的导体球体，所有球体共线，如图所示是 $ n=2 $ 情况的示意图. 每个球体与相邻球体的间距都是 $ d $ ， $ d $ 远大于球体半径因此将球体近似视作点电荷，所有的球体质量均为 $ m $ ，带 电量为 $ +Q $ 或 $ −Q $ . 球体与地面间最大静摩擦系数是 $ \mu $ ，重力加速度为 $ g $ ，静电力常数为 $ k $ . 已知最大静摩 擦系数 $ \mu $ 满足关系 $ kQ^2< \mu mgd^2< 2kQ^2 $ .
   
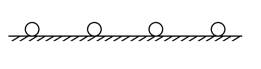
   1. 倘若每个球体与相邻球体的间距并不远大于球体的半径，计算球体间的静电力时能否将球体视为点电荷？试简要阐释原因. (4分)
   2. 若 $ n=2 $ ，试对所有球体可能带电的情况分别讨论体系是一定保持平衡、可能保持平衡还是一定不会 保持平衡. (5分)
   3. 若 $ n=4 $ ，试对所有球体可能带电的情况分别讨论体系是一定保持平衡、可能保持平衡还是一定不会 保持平衡. (16分)
3. 考虑竖直墙壁上附着的一个半径为 $ r $ 的实心半球形光源，其表面的每一点都向四周均匀发光，单位时间辐射 出去的光能为 $ P $ . 半球的球心距地面高 $ H $ ，如图所示. 人眼所观测到的亮度正比于单位时间垂直进入人眼的单位面积的光能. 不考虑空气对光能的吸收，没有特别说明的情况，墙壁与地面均不反光.
   
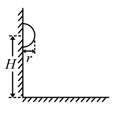
   1. 若水平地面由理想平面镜构成，则会发现半球光源的镜像的亮度总是低于半球光源本身的亮度，试简要阐述此现象的原因. (4分)
   2. 若水平地面由理想平面镜构成，试求平面镜单位时间内反射的光的能量. (5分)
   3. 考虑有一观察眼在车灯正前方与半球心距离 $ s $ 处，若观察眼正视光源时看到的亮度为 $ L_s $ . 现使该眼四处移动，但是保持其与半球心的距离不变，并始终正视车灯，如图所示，如果该眼在某个面积 $ A $ 内观察到车灯的亮度仍为$ L_s $ ，试求 $ A $ . (8分)
      
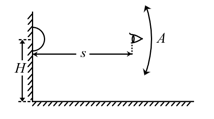
   4. 若在半球形光源正上方距半球心 $ l $ 处放置一个半径为 $ a(a\ll r) $ 的微型的球形能量接收器，该能量接收器会完全吸收照射在其上的光能，试求该能量接收器单位时间内接收到的光能. (8分)
4. 我们通常用 $ H $ 来代表热力学量焓. 任意处于平衡态的热力学体系的焓值为：\[H = U + pV\] 其中 $ U $ 是体系的内能， $ p $ 是体系的压强， $ V $ 是体系的体积.\\考虑一个密闭绝热容器，容器体积恒为 $ V_1 $ ，容器中充满可以视为理想气体的水蒸气，水蒸气的压强为 $ p_1 $ ，密度为 $ \rho_1 $ ，温度为 $ T_1 $ ，比热容为 $ c_1 $ . 初始时容器中另一 有一块体积为 $ V_0(V_0 \ll V_1) $ 的冰块，其温度为 $ T_0 $ ，密度为 $ \rho_0 $ ，比热容为 $ c_0 $ . 若冰块会在当前压强值下当温度达到 $ T_2(T_1 > T_2 > T_0) $ 时升华为水蒸气. 冰块升华为水蒸气需要吸收 $ Q $ 的热量. 由于冰块的体积很小，故冰块 升华前后可将容器内气体的压强视作恒为 $ p_1 $ .
   1. 试判断 $ Q $ 的正负，并简要阐述原因. (3分)
   2. 试求冰块从 $ T_0 $ 开始升温，直至升华为水蒸气并且整个容器达到热平衡时，整个系统的焓值的变化. (5分)
   3. 试求冰块从温度为 $ T_2 $ 的冰升华为温度为 $ T_2 $ 的水蒸气的过程中其内能的变化. (6分)
   4. 试求冰块从温度为 $ T_2 $ 的冰升华为温度为 $ T_2 $ 的水蒸气的过程中其焓值的变化. (6分)
   5. 试求体系最终达到热平衡后的温度. (15分)

第四届OPhO预赛参考答案

1. 1. 物块在 $ t = 0 $ 到 $ t = t_1 $ 内机械能守恒，在 $ t = t_1 $ 到 $ t = t_2 $ 内机械能减小.
   2. \[W=0\]
   3. \[\mu=\frac{\sqrt{2gh}}{g(t_2-t_1)}\]
   4. \[s=\frac{t_2}{2}\sqrt{2gh}\]
2. 1. 若每个球体与相邻球体的间距并不远大于球体的半径，不能将球体视为点电荷，因为由于导体球间的静电感应，球体上的电荷分布不是球对称分布，而此时将球体视为点电荷，计算它们之间静电力的结果将会有较大的误差.
   2. 若两个小球带电情况是 $ +-/++/-- $ ，体系一定平衡.
   3. 若四个小球带电情况是：$ ++++/---- $ ，体系可能平衡；$ +++-/---+/-+++/+--- $ ，体系一定不平衡；$ ++-+/--+-/-+--/+-++ $ ，体系可能平衡；$ ++--/--++ $ ，体系一定不平衡；$ +-+-/-+-+ $ ，体系一定平衡；$ +--+/-++- $ ，体系可能平衡；
3. 1. 理想平面镜中的半球形光源相距观察者更远，因此观察者接收到半球形光源的反射光的光能更小，故镜像的亮度更低.
   2. \[\frac{P}{4}\]
   3. \[A=2 \pi s^2-2 \pi \sqrt{s^4-s^2 r^2}\]
   4. \[\frac{Pa^2}{4l^2}\]
4. 1. $ Q >0 $ ，因为固体升华为气体需要吸热.
   2. \[\Delta H=p_1V_1\]
   3. \[\Delta U=Q-p_1V_1\]
   4. \[\Delta H=Q\]
   5. \[T=\frac{\rho_1 V_1 T_1}{\rho_0 V_0+\rho_1 V_1}+\left(1-\frac{c_0}{c_1}\right) \frac{\rho_0 V_0 T_2}{\rho_0 V_0+\rho_1 V_1}+\frac{c_0\rho_0V_0T_0-Q}{c_1(\rho_0 V_0+\rho_1 V_1)}\]

第四届OPhO决赛试题

解答题

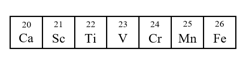
1. 质子与中子统称为核子，有一种描述核子状态的量称为同位旋. 每个质子的同位旋为 $ 1/2 $ ，每个中子的同位旋则为 $ −1/2 $ ，假设原子核的总同位旋等于所含核子的同位旋之和. 由光照射诱发的核反应，称为光核反应， 原子核吸收光能，可以裂变为质量更轻的核. 已知钒元素V的某种核素的原子核可以发生某种光核反应，裂变为一种较轻的核，这个过程使该原子核的核电荷数减 $ 1 $ ，同位旋数由 $ −5/2 $ 变为 $ −3/2 $ . 如图所示是钒元素V附近的元素周期表，元素符号上方的数字是元素的核电荷数. 已知真空光速为 $ c $ ，普朗克常数为 $ h $ .
   
   1. 写出此反应的核反应方程式. (4分)
   2. 某个实验使用光照射静止的这种钒原子核，发现反应使得生成物的总质量相比反应前的钒核质量增加了 $ \Delta m $ ，已知该核反应能量、动量均守恒（均为相对实验室参考系而言）. 试求生成物的总动量. (5分)
   3. 如果入射光的能量必须大于 $ E_m $ ，光核反应才能发生，则 $ E_m $ 称为反应的阈能，某个 实验通过测量反应生成物的质量相比钒核质量的增加来寻找此反应的阈能，测量发现该反应的阈能大致是 $ E_m $ . 现在提高测量质量 增加量的精度，设要求质量增量测量的不确定度小于 $ \delta E_m $ ，试求测量时间 $ \delta t $ 所应满足的不等式. (6分)
2. 在压强恒为 $ p_0 $ 的大气中飘浮着一个半径为 $ r_0 $ 的球形气球，气球内充斥一定量的两种双原子分子构成的理想气体，初始时气球处于静止平衡状态，此后气球内的两种理想气体开始发生化学反应，反应生成物是另外两种双原子分子理想气体，该反应释放能量，并且气球也开始膨胀，直至爆炸. 气球与外界大气的温度相等且恒定. 在膨胀过程中气球内气体向气球外放出了 $ Q(Q > 0) $ 的热量. 该气球的表面张力系数 $ \sigma $ 与气球半径 $ r $ 的关系为 $ \sigma=kr^2 $ ， $ k $ 为已知常数，气球爆 炸时的临界半径为 $ r_c $ .
   1. 试求气球从开始膨胀到临界爆炸整个过程内部气体的内能改变. (5分)
   2. 试求初始气球处于平衡状态时气球内部的压强. (6分)
   3. 试求气球从开始膨胀到临界爆炸整个过程内部气体发生化学反应释放的能量. (7分)
   4. 试求气球从开始膨胀到临界爆炸整个过程内部气体对气球做功. (7分)
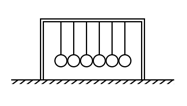
3. 有一个有 $ n(n > 2) $ 个小球的牛顿摆，固定在水平桌面上，如图所示是 $ n=6 $ 情况的示意图. 已知每个小 球的半径为 $ r $ ，吊线长均为 $ l(l\gg r) $ ，所有小球之间碰撞的恢复系数均为 $ e(0< e< 1) $ . 现保持吊线紧绷地将最左侧小球拉动 $ d(d\ll l) $ 后自由释放. 重力加速度为 $ g $ ，忽略空气阻力.
   
   1. 提起最左侧一颗小球到一定高度，使它自由摆下，直到另一端小球达到最高点，写出这个时间段内所有存在的能量形式及其之间的转化. (3分)
   2. 提起最左侧一颗小球释放后，牛顿摆在一个完整周期内的动量是否守恒？试简要阐述守恒或不守恒的原因. (3分)
   3. 若 $ n=2 $ ，试求第一次碰撞后左侧小球的速率. (5分)
   4. 若 $ n=2 $ ，试求两个小球在经历无穷长时间后的速率. (5分)
   5. 若 $ n=2 $ ，某时刻该牛顿摆的机械能是初始未碰撞时的 $ 1/k $ ，试求两球已碰撞的次数. (7分)
   6. 对一般的 $ n $ ，试求在经历无穷长时间后，牛顿摆的振幅. (7分)
4. 将一个电荷量为 $ q (q > 0) $ 的带正电点电荷固定于真空中的某点，再将一个电荷量为 $ −q $ ，质量为 $ m $ 的带负电点电荷以某一初速度释放，发现该负电荷恰好可以绕正电荷做半径为 $ r_0 $ 的匀速圆周运动. 已知静电力常数为 $ k $ ，不计电荷运动产生的磁场、相对论效应及辐射效应.
   1. 试求释放负电荷的初速度 $ v_0 $ . (3分)
   2. 若在负电荷绕正电荷做匀速圆周运动的过程中，突然将正电荷换成电荷量为 $ \lambda q(\lambda > 0) $ 的点电荷，发现负电荷恰好不能绕新放置的正电荷做周期性的运动，试定性说明负电荷的运动速率将如何变化. (4分)
   3. 在(2)的条件下，试求 $ \lambda $ . (6分)
   4. 若在负电荷绕正电荷做匀速圆周运动的过程中，在垂直于负电荷做圆周运动的轨道平面的方向上加一个在空间上均匀分布的磁场，磁感应强度大小随时间均匀缓慢地从 $ 0 $ 增加到 $ B_0 $ ，试判断在磁场增加期间负电荷是否有可能仍然保持原来的轨道继续做圆周运动，并证明你的结论. (9分)
   5. 在 (4) 的条件下，如果发现加完磁场后，负电荷的轨道半径和角速度变化都很小，即 $ \Delta r \ll r_0 $ 及 $ \Delta \omega \ll\omega_0 $ ，其中 $ \omega_0 $ 是加磁场前的轨道角速度. 试在一级近似下求负电荷做匀速圆周运动的轨道半径变化和角速度变化的大小. (13分)

第四届OPhO决赛参考答案

1. 1. \[\gamma+{ }_{23}^{51} \mathrm{V} \longrightarrow{ }_{22}^{47} \mathrm{Ti}+3{ }_0^1 \mathrm{n}+{ }_1^1 \mathrm{p}\]
   2. \[p=\Delta m c^2\]
   3. \[\delta t\leqslant \frac{h}{4\pi\delta E_m}\]
2. 1. 内能改变为0.
   2. \[p_0+2kr_0\]
   3. \[Q+2\pi k(r_c^4-r_0^4)+\frac{4\pi p_0}{3}(r_c^3-r_0^3)\]
   4. \[2\pi k(r_c^4-r_0^4)+\frac{4\pi p_0}{3}(r_c^3-r_0^3)\]
3. 1. 重力势能 $ \rightarrow $ 平动动能 $ \rightarrow $ 振动动能 $ \rightarrow $ 平动动能 $ \rightarrow $ 重力势能
   2. 动量不守恒. 因为牛顿摆固定在地面上，牛顿摆整体在一个周期中受到的合外力并不恒为0，不为0的合外力会改变动量.
   3. \[\frac{d}{2}\sqrt{\frac{g}{l}}(1+e)\]
   4. 两球速率均趋近于：\[\frac{d}{2}\sqrt{\frac{g}{l}}\]
   5. \[\frac{1}{2}\ln\left(\frac{2}{k}-1\right)\]
   6. 所有球一起摆动，振幅为：\[\frac{d}{n}\]
4. 1. \[v_0=q\sqrt{\frac{k}{mr_0}}\]初速度方向应与释放点和正电荷的连线垂直.
   2. 负电荷应做抛物线运动，速率减小.
   3. \[\lambda=\frac{1}{2}\]
   4. 负电荷不可能保持原轨道继续做圆周运动，证明略.
   5. \[\Delta\omega=\frac{qB_0}{2m}\]\[\Delta r=0\]