线上物理竞赛 Online Physics Olympiad

第三届OPhO预赛试题

解答题

1. 在光滑的水平地面上放置一个可以视为质点的质量为 $ m $ 的物块，初始 $ t = 0 $ 时刻质点处于静止状态，若在 $ t = t_1 $ 时刻开始给这质点施加一个大小为 $ F $ 的恒力，方向未知. 这个恒力的作用持续到 $ t = t_2 $ 时刻停止，物块运 动时始终不脱离水平地面，忽略一切阻力.
   1. 简要阐述什么是惯性. (1分)
   2. 试求物块 $ t=t_2 $ 时刻速度大小的取值范围. (1分)
   3. 试求物块在 $ t = 0 $ 到 $ t = t_2 $ 这个时间段内的路程的取值范围与平均速率的取值范围. (2分)
   4. 试求物块在 $ t = 0 $ 到 $ t = t_2 $ 这个时间段内的加速度大小的平均值的取值范围. (2分)
   5. 试求在 $ t = t_1 $ 到 $ t = t_2 $ 这个时间段内恒力的冲量的取值范围及恒力所做的功的取值范围. (4分)
2. 如图所示，在一根周长为 $ L $ 的圆形导线中间放置一根长为 $ l $ 的直导线，直导线作为圆导线的一根弦，直导线的两端与圆导线接触良好. 直导线与圆导线的材质、横截面积完全相同. 现在A点与B点两端加以恒定直流电压.
   
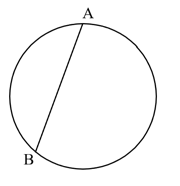
   1. 试求直导线、大圆弧、小圆弧三者中通过的电流之比. (5分)
   2. 在题述的基础上，给圆导线外接一个与圆导线材质、横截面积完全相同的导线构成的正五边形，即使圆内切于正五边形，试求一共能构成的不相互等价的等效电路的数目. (5分)
3. 一颗半径为 $ R $ 的恒与一颗半径为 $ r $ 的行星相距 $ l(l\gg r) $ ，如图所示. 恒星通过核聚变维持其高 温并通过热辐射的形式向外辐射能量. 理想的吸收与辐射物体称为黑体，黑体会将外来的辐射全部吸收而完全没有反射. 黑体单 位时间内从单位面积辐射出的热量 $ J $ 只与其热力学温度 $ T $ 有关，为 $ J = \sigma T^4 $ ，其中 $ \sigma $ 是一个基本常数，称为斯特藩-玻尔兹曼常数. 假设该恒星与该行星均可以视为黑体.
   
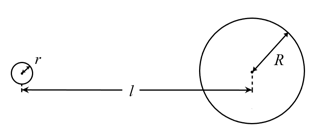
   1. 试求该行星表面接收不到该恒星发出的光照射的部分的面积. (4分)
   2. 若该行星的温度均匀且恒定不变，试求恒星表面温度与行星温度的比值. (7分)
   3. 有恒星光线照射和无恒星光线照射的分界线称为晨昏线. 如果某人站在该行星的晨昏线上，看到 恒星的形状恰好是个半圆，试估算该人的身高. (9分)
4. 某种特殊类型的质量为 $ m $ 的汽车，它启动后的牵引力功率 $ P $ 与行驶速度 $ v $ 恒满足如下函数关系：\[P=P_0+\frac{k}{v+\lambda}\]其中 $ P_0 $ 、 $ k $ 和 $ \lambda $ 是常数，其中 $ k $ 、 $ \lambda $ 为已知. 考虑该种汽车 在动摩擦系数为 $ \mu $ 的水平地面上行驶，最大静摩擦力等于动摩擦力，重力加速度为 $ g $ .
   1. 试求常数 $ k $ 在国际单位制中的单位. (2分)
   2. 试求 $ P_0 $ . (3分)
   3. 试证明 $ k\leqslant 0 $ . (4分)
   4. 若 $ \lambda > 0 $ ，试求该种汽车能够达到的最大速率以及此时汽车牵引力的功率. (5分)
   5. 试证明 $ \lambda > 0 $ . (6分)
5. 2004 年 1 月 22 日，中国台湾云林县的海面上出现了一个巨大的漂浮“球体”，这个在海面上漂浮“球体”实则是一头已经死亡的抹香鲸的头部，已知其质量为 $ m $ ，海水密度为 $ \rho $ ，重力加速度为 $ g $ ，海面附近的大气压强恒为 $ p_0 $ . 为简单起见，假设这个“球体”处于平衡位置时的大圆面和海面重合，海面是平静的，只考虑“球体”受到的重力和海水的浮力，假设“球体”内部是理想气体，“球体”漂浮在海面上平衡时内部的温度为 $ T_0 $ .
   1. 午后的海水温度通常低于海面附近空气的温度，试简要阐述原因. (2分)
   2. 试求此“球体”在海面上做微小的上下简谐振动的周期. (8分)

   · 人们试图用起重机吊起抹香鲸的 头部. 由于抹香鲸的头部离开了海水，以及午后天气炎热的缘故，“球体”的体积迅速增加. 当抹香鲸头部的体积足够大时，就会发生爆炸，俗称“鲸爆”.

   3. 试分析并解释原本体型越大的鲸鱼越容易发生“鲸爆”的原因. (8分)
   4. 假设“球体”内部气体的升温过程足够缓慢，当“球体”内部气体的温度达到 $ T $ 时，发生了鲸爆，试求 爆炸前瞬间“球体”的体积. (8分)
   5. 假设“球体”在被吊起的过程中发生了鲸爆. 记爆炸发生后瞬间为时刻 $ t = 0 $ ，此刻“球体”表面上各 点的速度大小都是 $ v_0 $ ，方向背离其与球心的连线. 试求在爆炸发生后且爆炸的碎片未落地前的某时刻 $ t $ ，球体的表面碎片在空中构成的图形在直角坐标系下的曲面方程. (14分)

第三届OPhO预赛参考答案

1. 1. 物体保持静止状态或匀速直线运动状态的性质，称为惯性.
   2. \[v\in\left[0,\frac{F}{m}(t_2-t_1)\right]\]
   3. \[s\in\left[0,\frac{F}{2m}(t_2-t_1)^2\right]\]\[\bar{v}\in\left[0,\frac{F(t_2-t_1)^2}{2mt_2}\right]\]
   4. \[\bar{a}\in\left[0,\frac{F(t_2-t_1)}{mt_2}\right]\]
   5. \[W\in\left[0,\frac{F^2}{2m}(t_2-t_1)^2\right]\]\[I\in\{F(t_2-t_1)\}\]
2. 1. 直导线、大圆弧、小圆弧三者中通过的电流之比为：\[\frac{1}{l}: \frac{\pi}{L\left(\pi-\arcsin \frac{l \pi}{L}\right)}: \frac{\pi}{L \arcsin \frac{l \pi}{L}}\]
   2. 不等价的等效电路有4种.
3. 1. 行星接收不到光照射部分的面积为：\[2 \pi r^2 \left(1-\frac{l}{R-r}\right)\]
   2. 恒星表面温度与行星温度的比值为：\[\sqrt[4]{\frac{4l^2}{R^2}}\]
   3. 该人身高约为：\[\frac{(R-r)r}{\sqrt{l^2-R^2}}-r\]
4. 1. \[[k]=\mathrm{kg\cdot m^3/s^4}\]
   2. \[P_0=-\frac{k}{\lambda}\]
   3. 汽车启动时牵引力一定有 $ F \geqslant 0 $ ，从而可以证明 $ k\leqslant 0 $ . 证明略.
   4. 若：\[-\frac{k}{\lambda^2} >\mu mg\]最大速率为：\[v_m=\frac{-k}{m\lambda \mu g}-\lambda\]此 时牵引力功率为：\[P=-\frac{k}{\lambda}-m\mu g\lambda\]若：\[-\frac{k}{\lambda^2}\leqslant \mu mg\]最大速率为：\[v_m=0\] 此时牵引力功率为：\[P=0\]
   5. 根据汽车的牵引力、牵引力功率、加速度应有界，可以证明 $ \lambda > 0 $ . 证明略.
5. 1. 因为海水的比热容大于空气，所以空气升温比海水快，故海水的温度较低.
   2. \[T=\frac{2}{3} \sqrt[3]{18} \pi^{{5}/{6}} \rho^{-{1}/{6}} m^{{1}/{6}} g^{-{1}/{2}}\]
   3. 根据理想气体状态方程，升高相同的温度时，体积为 $ V_1 $ 与 $ V_2 $ 的“球体”的体积变化：\[\frac{\Delta V_1}{\Delta V_2}=\frac{V_1}{V_2}\]故它们的半径 $ R_1 $ 与 $ R_2 $ 的变化满足：\[\frac{\Delta R_1}{\Delta R_2}\sim \frac{R_1}{R_2}\]表面积变化则为：\[\frac{\Delta S_1}{\Delta S_2} \sim \frac{R_1 \Delta R_1}{R_2 \Delta R_2} \sim \frac{R_1^2}{R_2^2}\]可见原本体积越大的，表面积变化也越大，所以自身更容易“爆炸”.
   4. \[V=\frac{2mT}{\rho T_0}\]
   5. 以竖直向上为 $ z $ 轴正方向建立直角坐标系，则 $ t $ 时刻碎片在空中构成的曲面方程为：\[x^2+y^2+\left(z+\frac{1}{2} g t^2\right)^2=\left(\sqrt[3]{\frac{3 m T}{2 \pi \rho T_0}}+v_0 t\right)^2\]

第三届OPhO决赛试题

解答题

1. 假设在密闭容器内盛有一定量某种物质的液体，当从液体表面蒸发出去的液体物质分子与从液体上方的气体中进入液体的物质分子达到平衡时，称液体上方的该种物质的气体为饱和蒸气. 在同一温度下，一种物质的饱和蒸气所产生压强称为饱 和蒸气压. 另一方面，已知理想气体在单位时间内碰撞到单位面积的容器壁或液体表面上的分子个数由以下公式描述：\[N=\frac{p}{\sqrt{2\pi mT}}\]其中 $ p $ 为该理想气体的压强， $ m $ 为该种理想气体分子的质量， $ T $ 为气体的热力学温度.
   1. 当液体温度降低，试确定其上的饱和蒸气压如何变化，并简要阐释原因. (2分)
   2. 考虑分子质量为 $ m_0 $ 的某种物质，该种物质的液体在温度 $ T_0 $ 下的饱和蒸气压为 $ p_0 $ ， 设单位时间内从该种液体的表面单位面积上蒸发到真空中的分子数为 $ N_0 $ ，则有：\[N_0< \frac{p_0}{\sqrt{2\pi m_0T_0}}\]试证明此结论. (3分)
2. 考虑一根某种材料制成的均质圆柱体. 将圆柱体放在地面上，当两端同时施加大小为 $ F $ 的平行于圆柱轴线的 拉力时，圆柱中间某处恰好会断裂. 现将圆柱其中一端固定在竖直墙壁上，其余的部分垂直于竖直墙壁，如图所示，此时发现圆柱也恰好会在某处断裂.
   
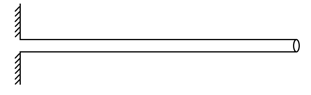
   1. 试简要阐述当圆柱一端固定在墙壁上，圆柱会断开的原因. (3分)
   2. 使用同种材料制作另外一根长度为原先的 $ n $ 倍的圆柱体，同样将圆柱一端垂直于竖直墙壁固定，若 新制成的圆柱不会断裂，试估算其半径至少是原先的多少倍. (5分)
   3. 考虑在圆柱密度不变的情况下，对圆柱材料进行加固，并增加圆柱的半径与长度使体积到原来的 $ n $ 倍，将新制成的圆柱放在地面上，发现给该圆柱体两端施加 $ kF $ 的拉力时，该圆柱恰好会从中间某处断开. 将该圆柱体一端垂直于竖直墙壁固定，发现圆柱恰好会断开，试估算圆柱的截面积是原先的多少倍. (6分)
   4. 若从圆柱体的中间挖取出一个半径为原先 $ 1/n $ 的与大圆柱同轴的小圆柱，将该圆环柱体的一端垂直 于竖直墙壁固定，并在保持内外半径不变的前提下继续加长这个圆环柱体，试估算这个圆环柱体可以保持不断裂的最大长度是原先的多少倍. (6分)
3. 考虑如图所示的一个均质的边长为 $ d $ 的正方体物块在粗糙水平地面上滑动，参考点O选取在地面上，正方体心、参考点、正方体速度方向三者共面，已知地面的动摩擦系数为 $ \mu $ ，正方体质量为 $ m $ ，重力加速度为 $ g $ .
   
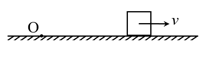
   1. 若某时刻正方体的滑动速度大小为 $ v $ ，正方体重心与O点间的水平距离为$ l $ ，指出该正方体上对参考点角动量最小与最大的点分别是哪些点，并求这些点附近的单位质量的角动量大小. (3分)
   2. 若正方体在地面上滑动不会翻倒，试求动摩擦系数为 $ \mu $ 的取值范围. (5分)
   3. 若正方体在地面上滑动不会翻倒，试求地面对正方体的摩擦力合力的作用点与正方体重力作用点的距离. (5分)
   4. 若正方体在地面上滑动不会翻倒，设正方体重心与参考点O点间的水平距离为 $ l $ ，已知当 $ l=0 $ 时，正方体滑动速度为 $ v_0 $ ，试求之后正方体角动量相对于参考点O的角动量大小与 $ l $ 的关系式. (7分)
4. 我们定义反应截面为描述发生某种反应的概率的物理量，反应截面 $ \sigma $ 可以通过以下公式计算：\[\sigma=\frac{R}{ndIS}\]其中 $ I $ 称为粒子流强度，定义为单位时间内通过单位截面积上的入射粒子个数， $ n $ 为单位体积的靶内所包含的靶核数目， $ S $ 为靶面的面积， $ d $ 为靶的厚度， $ R $ 为单位时间发生这种核反应的次数，同一种核反应的反应截 面是一定的.\\假设有一种粒子K，会与一种原子核T发生核反应并生成一个第三种粒子 $ \Theta $ 并释放大量能量（假设生成的粒子对 反应没有影响）. 现考虑有一种核反应装置，由原子核T构成的靶面为一系列的同心球面，这些靶面的半径为 $ r,2r,3r,\dots ,nr $ ，每个靶面的厚度为 $ d(d\ll r) $ ，由于靶很薄，靶上的原子核不会存在前后遮挡的现象，所有靶面上的靶核个数均为 $ N_0 $ 且为常数. 在这些靶面的球心处有一个向四面八方发射粒子K的装置，单位时间内这个装置会以随机方向向四周发射 $ N $ 个K粒子.
   1. 写出粒子K与原子核T发生反应的反应方程式. (1分)
   2. 不考虑K粒子在靶面上的反射，若粒子K与靶核T的反应截面为 $ \sigma $ ，试求单位时间内在第一个靶 面上发生的反应数. (5分)
   3. 不考虑K粒子在靶面上的反射，试求在单位时间内第 $ m $ 个靶面及之前所有靶面的总反应次数. (9分)
   4. 考虑K粒子在靶面上的反射，若粒子在靶面上反射流的强度为 $ I^{\prime}=c I \varsigma $ ，其中 $ I $ 为入射粒子流强度， $ c $ 为反射率，可视为一个常数， $ \varsigma $ 为靶面上单位面积的靶核的个数. 现在已知该反应体系平稳时，单位时间内第一个靶面上的反应次数为 $ R_1 $ ，反射率 $ c $ 已知，试求从外部靠近第一个靶面的K粒子流的强度. (10分)
5. 考虑空间中存在匀强磁场，磁感应强度大小为 $ B $ . 在竖直平面内建立直角坐标系 $ Oxy $ ，使 $ y $ 轴正 方向竖直向上， $ x $ 轴正方向水平向右，匀强磁场方向垂直 $ Oxy $ 平面向里. 坐标原点 $ O $ 处有一个粒子源，可以在 $ Oxy $ 平面内以任意方向发射任意速度的质量为 $ m $ ，电荷量为 $ q $ 的带正电粒子. 重力加速度为 $ g $ . 不计相对论效应.
   1. 如果粒子源发射的粒子可以沿着 $ x $ 轴做匀速直线运动，试求粒子的初速度大小. (1分)
   2. 如果粒子源将粒子无初速度发射，那么粒子运动的轨迹将会与 $ x $ 轴相交于一组点，其坐标通式为 $ (c_n, 0) $ ，记 $ O $ 点处为 $ c_0 = 0 $ ，试求数列 $ {c_n} $ 的通项公式. (6分)
   3. 如果粒子源将粒子以大小为 $ v_0 $ ，方向与 $ x $ 轴正方向成 $ \theta $ 角的初速度发射，而粒子运动的轨迹将会与 $ x $ 轴相交于一组点，试求这组点的坐标. (11分)
   4. 如果粒子源将粒子以大小为 $ v_0 $ ，方向与 $ x $ 轴正方向成 $ \theta $ 角的初速度发射，试求粒子速率的最大值及粒子速率达到最大值时这些点的坐标. (12分)

第三届OPhO决赛参考答案

1. 1. 当温度降低时，液体中的分子平均动能减小，因此相同时间内有足够的能量能够从液体表面克服分子间吸引力，逃逸出液体表面，变成气体分子的分子数也就更少. 而气体的液化与液体的蒸发达到平衡，说明气体进入液体中的分子数也就更少，因此气体分子数的密度也就更小，气体压强的产生机制是气体分子的碰撞，所以此时的压强也就更小，因此液体温度降低，饱和蒸气压会减小.
   2. 若液体上方的气体达到饱和，则进入液体的分子数和从液体中逸出的分子数相等. 而在气体中碰到液体表面的分子不一定都会进入液体，也有可能会发生“反射”，返回气体中，设这个反射的概率为 $ R $ ，那么单位时间内，进入到液体表面 单位面积的分子数为：\[N_0=\frac{p_0}{\sqrt{2\pi m_0T_0}}(1-R)\]考虑到 $ 0< R< 1 $ ，故：\[N_0< \frac{p_0}{\sqrt{2\pi m_0T_0}}\]
2. 1. 以圆柱与墙壁的接触点为支点，重力会使圆柱有转动的趋势，而抵抗这个效果的另一个力是圆柱体内部对圆柱向左的力. 两个力的力与力臂乘积相等才使圆柱平衡. 但是圆柱体内部的力有一个最大限度，当内部的力超过这个最大限度，圆柱就会断开.
   2. \[n^2\]
   3. \[n^{-{4}/{3}}k^{{2}/{3}}\]
   4. \[1\]
3. 1. 正方体上表面与速度 $ v $ 平行的两条边上的点是角动量最大的点，角动量大小为：\[\frac{\sqrt{5}}{2}vd\]参考点与正方体体心的速度所在面与正方体底面交线上的点是角动量最小的点，角动量大小为0.
   2. \[\mu\in [0,1)\]
   3. 作用点之间的距离为：\[\frac{\sqrt{\mu^2+1}}{2}d\]
   4. \[L=\frac{mv_0d}{2}+\frac{m d\left(v_0-\sqrt{v_0^2-2 \mu g l}\right)}{2 \mu }\]
4. 1. \[\mathrm{K+T}\longrightarrow \Theta+\gamma\]
   2. \[\frac{NN_0}{4\pi r^2}\sigma\]
   3. \[N \sum_{n=1}^m \frac{N_0 \sigma}{4 \pi(n r)^2} \prod_{i=0}^{n-1}\left[1-\sigma \frac{N_0}{4 \pi(i r)^2}\right]\]
   4. \[\frac{16 \pi^2 r^4 R_1-4 \pi N r^2-c N N_0}{32 \pi^2 r^4-4 \pi r^2 N_0(\sigma+c)}\]
5. 1. \[v_0=\frac{mg}{qB}\]
   2. \[c_n=\frac{2\pi nm^2g}{q^2B^2}\]
   3. \[\left\{\left(-\frac{2 m v_0 \sin \theta}{q B}+\frac{2 m^2 g \arcsin \left(q B v_0 \sin \theta / m g\right)}{q^2 B^2}+\frac{2 \pi n m}{q B}, 0\right) \cup\right.\left.\left.\left(\frac{2 \pi n m^2 g}{q^2 B^2}, 0\right) \right\rvert\, n=0,1,2, \cdots\right\}\]
   4. \[\{(x_n,y_n)\rvert\ n=0,1,2, \cdots\}\]\[x_n=-\frac{2 m v_0 \sin \theta}{q B}+\frac{2 m^2 g \arcsin \left(q B v_0 \sin \theta / m g\right)}{q^2 B^2}+\frac{(2 n+1) \pi m}{q B}\]\[y_n=-\frac{m^2 g}{q^2 B^2}-\sqrt{\frac{m^4 g^2}{q^4 B^4}+\frac{m^2}{q^2 B^2} v_0^2-\frac{2 m^3 g}{q^3 B^3} v_0 \cos \theta}+\frac{m v_0}{q B} \cos \theta\]