线上物理竞赛 Online Physics Olympiad

第二届OPhO预赛试题

一. 填空题：每题8分

1. 电磁波的波长$\lambda$、波速$c$及频率$f$之间的关系为______.
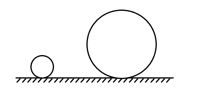
2. 考虑如图所示的两个同种材质的质地均匀的实心球静止放置在水平地面上，左侧球的半径为$R$，右侧球的半径为$nR(n>1)$，规定以水平地面为重力势能为0的平面. 若同时使两球的重心上升$R$的高度，则右侧球的重力势能是左侧球的______倍.
   
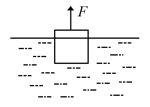
3. 如图所示，一个边长为$d$的均质的正方体平衡地漂浮在密度为$\rho$的液体的表面上，露出水面的体积是总体积的$1/4$. 重力加速度为$g$. 某人现以变力匀速上拉该正方体，当正方体有一半露出水面时，该人的拉力对正方体做功为______.
   
4. 某半径为$R$的圆形管口竖直向上喷出水柱，水刚喷出管口时的速率为$v$，假设水柱的横截面积$S$与喷射高度$h$的关系式为$S=\pi R^2+kh$，$k > 0$为已知常数. 忽略空气阻力及水的表面能，重力加速度为$g$. 若水柱喷射到高度为$H$时，分散成了半径为$r$的小水珠，则在这个高度处单位体积内的小水珠数量为______.
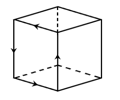
5. 考虑真空中的由12条导体细棒构成的正方体边框，给导体棒通以电流，若已知每根导体细棒上的电流大小是$I$或$I/2(I\neq 0)$，且有其中一个面的4条边上的电流方向已知（大小未知）如图所示. 则正方体框的顶面面心的磁感应强度大小的可能性共计有______.
   

二、解答题

6. 考虑某一种粒子A每单位时间会有总粒子数的 $ 1/p $ 将衰变为 $ q(q >1) $ 个粒子B，粒子B的平均寿命为 $ \tau $ ，粒子B会衰变为其它与问题无关的粒子. 考虑某个反应器械中于初始 $ t=0 $ 时刻有 $ N $ 个粒子A，现以某恒定速率从器械中 吸出粒子A，单位时间内吸出粒子A的个数为 $ n $ .
   1. 试写出粒子A发生衰变的反应方程式. (3分)
   2. 试求反应器械内粒子B的数量首次达到最大值时，粒子B的数量与粒子A的数量的比值. (5分)
   3. 试求反应器械内粒子A的数目关于时间的函数表达式 $ N_A(t) $ . (7分)
7. 我们通常用 $ S $ 代表物理量熵，理想气体的熵 $ S $ 可以通过以下公式进行计算：\[S=-N k\ln p-N k\chi(T)\]其中 $ N $ 为理想气体的分子数， $ p $ 为理想气体的压强， $ \chi(T) $ 为某个只依赖于理想气体热力学温度 $ T $ 的 函数， $ k $ 为玻尔兹曼常数.\\考虑两个用阀门连接的密闭绝热容器，容器体积分别恒为 $ V_1 $ 和 $ V_2 $ ，容器内分别装有分子数 $ N_1 $ 和 $ N_2 $ 的不同种类单原子理想气体. 阀门初始时关闭.
   1. 若两个容器内气体初始温度均为 $ T $ ，现打开阀门混合气体，试求最终达到平衡态的压强. (4分)
   2. 若两个容器内气体初始温度分别为 $ T_1 $ 和 $ T_2 $ ，现打开阀门混合气体，试求最终达到平衡态的压强. (4分)
   3. 若两个容器内气体初始温度均为 $ T $ ，且 $ V_1=V_2=V $ ，现打开阀门混合气体，试求最终达到平衡态后总熵的改变. (6分)
   4. 若两个容器内气体初始温度均为 $ T $ ，且 $ N_1=N_2=N $ ，现打开阀门混合气体，试求最终达到平衡态后总熵的改变. (6分)
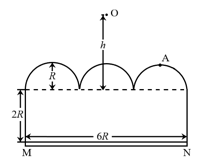
8. 如图所示，真空中一块长方体玻璃砖上放有三个相贴放置的截面为半圆形的柱状玻璃砖，半圆的半径均为 $ R $ . 中间的玻璃砖圆心处正上方 $ h $ 处有一点光源O，长方体玻璃砖高为 $ 2R $ ，长为 $ 6R $ . 所有玻璃砖的折射率均相同，长方体 底面MN为一接收屏. 发现当 $ h=2R $ 时，从A点和入射进入柱状玻璃砖的光线恰好不能进入长方体玻璃砖.
   
   1. 试求玻璃砖的折射率. (5分)
   2. 若从光源O发出某光线a和某光线b经过一次反射均可以回到O点，且光线a从O发出再到回到O点的用时是光 线b光从O发出再回到O的2倍，试求计算光线a从长方体玻璃砖出射时的折射角关于 $ h $ 的关系式. (6分)
   3. 现使 $ h\rightarrow \infty $ ，试求接收屏MN上接收到的光斑的宽度. (6分)
   4. 倘若光屏MN上只接收到一个光斑，试求这个光斑在MN方向上可能的最大宽度. (8分)

第二届OPhO预赛参考答案

1. \[c=\lambda f\]
2. \[\frac{n^3(1+n)}{2}\]
3. \[\frac{\rho gd^4}{32}\]
4. \[\frac{3vR^2}{4r^3(\pi R^2+kH)\sqrt{v^2-2gH}}\]
5. \[6\]
6. 1. \[A\longrightarrow qB\]
   2. \[\frac{q \tau}{p}\]
   3. \[(N+np)\mathrm{e}^{-t/p}-np\]
7. 1. \[\frac{kT(N_1+N_2)}{V_1+V_2}\]
   2. \[\frac{k(T_1+T_2)(N_1+N_2)}{2V_1+2V_2}\]
   3. \[N_1\ln\frac{2N_1}{N_1+N_2}+N_2\ln\frac{2N_2}{N_1+N_2}\]
   4. \[2N\ln\left(\frac{V_1+V_2}{2\sqrt{V_1V_2}}\right)\]
8. 1. \[n=\frac{2\sqrt{10}}{5}\]
   2. \[\theta=\frac{2\sqrt{10}}{5}\frac{h+R}{2h+R}\]
   3. \[\left(\frac{12\sqrt{15}}{5}-6\right)R\]
   4. \[6R\]

第二届OPhO决赛试题

一. 填空题：每题4分

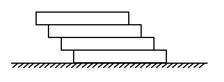
1. 考虑在水平桌面上放置一本质地均匀的长方体书，并在它上面继续放置完全相同的书，每本书的的边缘都超出前一本书的$1/b(b\geqslant 2, b\in \mathbb{Z})$，如图所示. 记最下方的书为第一本. 则至少能保证当放下第______本书时，书一定会倾倒.
   
2. 沙漠中有两只同一物种的动物. 动物A的体积是动物B的体积的一半. 当两只动物在沙漠中同时开始奔跑，假设它们身体的散热效率正比于体表表面积. 计及它们奔跑时需要克服空气阻力做功，空气阻力正比于相对空气的速率的平方与迎风面积，其它条件对两只动物无异. 则估算动物B奔跑直至体能耗尽的用时与动物A因奔跑导致体能耗尽的用时之比为______.
3. 有一个充满单原子理想气体的恒温恒压巨大热源，温度为$T$，现联通热源与一空的小容器，使热源气体的一小部分流入空容器中，则气体进入小容器后的温度与进入前的温度之比为______.
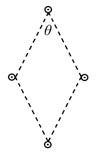
4. 如图所示，真空中的4条无限长平行直导线，均通以等大的垂直纸面向外的电流. 在垂直于电流方向的平面内，4条导线的连线恰好构成一个菱形，若菱形中点的磁感应强度为0，则该菱形任意一内角的余弦值为______.
   
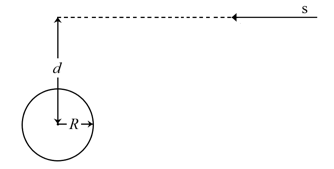
5. 考虑如图所示的真空中的质量为$M$，半径为$R$的均匀球体，一束光线s自无穷远处发射，光线所在直线到球体球心的距离为$d(d>R)$. 当光线接近球体时，会因为引力透镜镜效应而偏离原本所在直线. 牛顿引力常数为$G$，真空光速为$c$.光线s入射无穷远的渐近线和出射无穷远的渐近线之间的夹角约为______.
   

二、解答题

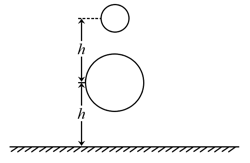
6. 考虑两质地均匀的球，较小球的半径为 $ R $ ，较大球的半径为 $ 2R $ ，较大球的密度是较小球的2倍. 较大球的球心距离地面 $ h(h >3R) $ ，较小球的球心在较大球球心正上方 $ h $ 处，如图所示，二者同时无初速度地释放，已知该情况下， 现知两球之间、两球与地面之间的恢复系数均为 $ e $ . 忽略空气阻力，碰撞过程的用时可以忽略，重力加速度为 $ g $ .
   
   1. 试求两球第一次碰撞后的瞬间较大球的速率. (4分)
   2. 试求两球第一次碰撞后较小球反弹后达到的最高点时球心与地面的距离. (6分)
7. 在真空中以 $ 1\rm m $ 为单位长度建立直角坐标系 $ Oxyz $ ，在点 $ (−1, 0, 0) $ 和 $ (1, 0, 0) $ 处各 固定放置一个电荷量为 $ q(q > 0) $ 的点电荷. 静电力常数为 $ k $ . 本题中长度单位 $ \rm m $ 可以省略不写.
   1. 试求点 $ (0, 1, 0) $ 处的电场强度大小. (1分)
   2. 若将一电荷量为 $ −q $ 的粒子从点 $ (0, 1, 0) $ 处由静止释放，试求粒子在 $ y > 0 $ 区域内的加速度最大的点P的坐标. (5分)
   3. 现拿走点 $ (−1, 0, 0) $ 处的点电荷，在平面 $ x = −1 $ 内放置一个无限大的起初不带电的接地导体平板. 等待稳定后，导体平板上将产生感应电荷，试求稳定后，在(2)中的点P处的电场强度. (8分)
   4. 在(3)的基础上，再在平面 $ x = 2 $ 内放置一个无限大的起初不带电的接地导体平板，试求稳定后为固定点 $ (1, 0, 0) $ 处的点电荷所需要施加的约束力 $ \vec{N} $ 的表达式. (11分)
8. 考虑在一个很大的平面板上方的密度为 $ \rho $ 的液体湍流，液体的运动黏度为 $ \nu $ . 若单位面积的平板 受到湍流液体引起的摩擦力为 $ \sigma $ ，则在本情景下可以定义一个特征速度 $ u=\sqrt{\sigma/\rho} $ 和一个特征距离 $ d=\nu/u $ . 本题中以 $ y $ 表示某点到平面板的距离. 那么在 $ y >d $ 的某处的液体流动的平均速度大小 $ v $ 可以总结为公式：\[v=\frac{u}{\varkappa}(\ln y+c)\]其中 $ \varkappa \approx 0.4 $ 称为卡门常数， $ c $ 是一个待定常数. 而 $ y< d $ 的某处的液体流动的平均速度大小 $ v $ 与该点到板的距离 $ y $ 成正比. 而在 $ y=d $ 附近，液体的平均速度大小 $ v=u/\varkappa $ .
   1. 试确定待定常数 $ c $ ，并明确写出 $ v(y) $ 的函数表达式. (5分)
   2. 如果平面板十分粗糙，上面有尺度数量级为 $ \epsilon $ 的小突起，实验发现，这种情况下 $ y >d $ 处液体流动平均速度 $ v $ 与运动黏度 $ \nu $ 无关. 已知此时 $ v(y) $ 的函数表达式的形式是 $ v=A\ln B $ ，并且 $ A $ 与(1)中的 $ y >d $ 的 $ v(y) $ 公式中的对数函数系数一致，试确定 $ B $ . (5分)

   · 实验表明，以上结果可以用于管道中湍流液体平均速度的计算，将管道的管壁看作无限多个小平板拼接而成即可. 已知某个圆形长直管道的半径为 $ r $ ，内部流动着密度为 $ \rho $ ，运动黏度为 $ ν $的湍流液体，并且管道中距离为 $ l $ 的两点压强差为 $ p $ .

   3. 若管壁并不粗糙，试求管道中轴线上流动的平均速度大小 $ U $ . (7分)
   4. 若管壁粗糙，其上有尺度量级为 $ \epsilon $ 的小突起. 定义管道的阻力因子为 $ \lambda=4rp/(l\rho U^2) $ . 试求此时管道的阻力因子，用参数 $ r $ 、 $ \epsilon $ 表示之. (9分)

   · 现在考虑在一个半无穷大平面板上方 的密度为 $ \rho $ 的液体湍流. 液体的运动黏度为 $ \nu $ ，单位面积的平板受到湍流液体引起的摩擦力为 $ \sigma $ . 特征量 $ u $ 与 $ d $ 的定义不变. 若在远离平板的上方，液体平均流速将几乎不受平板的影响而不依赖于高度 $ y $ ，且其值接近于某个无穷远来流的速度 $ V $ ，而我们记平均流速 $ v $ 达到 $ V $ 时的点距离平板的高度为 $ \delta $ ，而且 $ \delta $ 随着所在点与 板边缘的距离 $ x $ 的变化也在改变，其变化率满足公式：\[\lim _{\Delta x \rightarrow 0} \frac{\Delta \delta}{\Delta x}=\frac{u}{V}\]此时如果将 $ \sigma $ 看作不依赖于 $ x $ 的常数，并定义此情景下的阻力因子为：\[\varsigma=\frac{2\sigma}{\rho V^2}\]

   5. 试求 $ \delta $ ，用参数 $ \varsigma $ 、 $ x $ 表示之. (9分)
   6. 若平面板粗糙，其上有尺度量级为 $ \epsilon $ 的小突起，试求 $ \varsigma $ 、 $ \epsilon $ 、 $ x $ 三个参数之间的关系式. (10分)

第二届OPhO决赛参考答案

1. \[b+2\]
2. \[\sqrt[3]{2}:1\]
3. \[\frac{5}{3}\]
4. \[\frac{1}{3}\]
5. \[\frac{4GM}{c^2d}\]
6. 1. \[\left|\left(-\frac{e^2}{2}+\frac{15}{2} e-\frac{1}{2}\right) \sqrt{2 g(h-2 R)}-\frac{17 g(h-3 R)}{2(1+e) \sqrt{2 g(h-2 R)}}\right|\]
   2. \[\left[\left(\frac{e^2}{2}+\frac{17}{2} e-\frac{1}{2}\right) \sqrt{h-2 R}-\frac{17(h-3 R)}{4(1+e) \sqrt{h-2 R}}\right]^2+h+2 R-\frac{h-3 R}{1+e}+\frac{(h-3 R)^2}{4(1+e)^2(h-2 R)}\]
7. 1. \[E=k\frac{\sqrt{2}q}{2}\]
   2. \[\left(0,\frac{\sqrt{2}}{2},0\right)\]
   3. \[E_{\mathrm{P}}=-{kq}\left(\frac{2 \sqrt{6}}{9}+\frac{6 \sqrt{38}}{361}\right) \vec{e}_x+{kq}\left(\frac{2 \sqrt{3}}{9}+\frac{2 \sqrt{19}}{361}\right) \vec{e}_y\]
   4. \[\vec{N}=\frac{kq^2}{36}\left[-\frac{5}{4}+\frac{\pi^2}{6}-{\psi^{(1)}\left(\frac{1}{3}\right)}\right]\vec{e}_y\]\[\psi^{(1)}(x)=\frac{\mathrm{d}}{\mathrm{d}x}\left[\ln\Gamma(x)\right]\]
8. 1. \[c=-\ln\left(\mathrm{e}^{\varkappa}\frac{\nu}{u}\right)\]\[v= \begin{cases}\frac{u^2 y}{\varkappa \nu} & \left(y \leq d \right) \\ \frac{u}{\varkappa}\ln\left(\mathrm{e}^{\varkappa}\frac{y}{d}\right) & \left(y >d\right)\end{cases}\]
   2. \[B=\frac{y}{\epsilon}\]
   3. \[U=\sqrt{\frac{r p}{2 \varkappa^2 \rho l}} \ln \left(\frac{r}{\nu} \sqrt{\frac{r p}{2 \rho l}}\right)\]
   4. \[\lambda=\frac{8 \varkappa^2}{\ln ^2(r / \epsilon)} \]
   5. \[\delta=x \sqrt{\frac{\varsigma}{2}}\]
   6. \[\sqrt{\frac{2 \varkappa^2}{\varsigma}}=\ln \frac{x \sqrt{\varsigma}}{d}\]