线上物理竞赛 Online Physics Olympiad

第一届OPhO试题

一. 单选题：在每道题的4个选项中，有且仅有1个选项是符合题意的，每题5分

1. 考虑某颗特殊的行星，其可视作密度为 $ \rho $ ，半径为 $ R $ 的均匀实心圆柱体，圆柱的高远远大于其半径. 若欲从行星表面发射一颗卫星S使之绕圆柱做圆轨道运动，如图所示，则该行星的第一宇宙速度为______. 牛顿引力常数为 $ G $ .
   
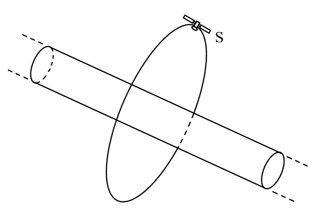
   1. $ R\sqrt{\pi G\rho} $
   2. $ R\sqrt{2\pi G\rho} $
   3. $ R\sqrt{3\pi G\rho} $
   4. $ R\sqrt{4\pi G\rho} $
2. 考虑某种核反应堆，其内部发生的核反应是通过某种元素X的原子核俘获周围单独的中子而发生的，每当X原子核俘获一个中子，便会发生反应立即释放出三个中子. 而且一个原子核发生核反应的概率与周围中子浓度成正比. 现假设某一台该种反应堆的反应过于缓慢，即单位时间核反应数太少，下列措施中不可能显著增加该反应堆核反应的剧烈程度的是______.
   1. 由于发生核反应会放出三个中子，所以将反应堆内的一部分中子换成X原子核
   2. 由于发生核反应概率正比于中子浓度，所以将反应堆内的一部分X原子核换成中子
   3. 由于发生核反应会放出三个中子，所以保持中子浓度不变和X原子核数不变，减小反应堆的体积
   4. 由于发生核反应概率正比于中子浓度，所以保持中子数目不变和X原子核浓度不变，减小反应堆的体积
3. 一罐温度为 $ T $ 的气体盛装在水平面上的静止容器中，初始时，容器左器壁的温度 $ T_1 >T $ ，容器右器壁 的温度 $ T_2< T $ ，则初始时气体对左器壁的压强 $ p_1 $ 与气体对右器壁的压强 $ p_2 $ 的大小关系为______.
   1. $ p_1 >p_2 $
   2. $ p_1< p_2 $
   3. $ p_1=p_2 $
   4. 无法判断
4. 在如图所示的直流电路中，四只电灯完全相同，三个电感线圈完全相同，闭合开关S，等到电路稳定后，断开S，则断开的瞬间四只电灯的亮度关系为______.
   
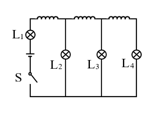
   1. $ \rm L_1 >L_2 >L_3 >L_4 $
   2. $ \rm L_2 >L_3 >L_4 >L_1 $
   3. $ \rm L_3 >L_2=L_4 >L_1 $
   4. $ \rm L_2 >L_3=L_4 >L_1 $

二. 填空题：每题5分

5. 在温度为$T_1$的高温热源和温度为$T_2$的低温热源之间工作的卡诺热机的热机效率为______.
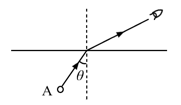
6. 某眼在水面上方观察水下的物体A，如图所示，若物体A进入人眼的光线在水下与水面的法线夹角为$\theta$，水的折射率为$n$，空气折射率为$1$，则人眼观察物体A的视觉深度与物体A的实际深度之比为______.
   
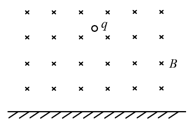
7. 如图所示，空间中有垂直于纸面向内的磁感应强度大小为$B$的匀强磁场. 考虑将一个质量为$m$的带电量为$q(q>0)$的点电荷从距离水平地面高$h(qBh < mv)$的位置以初速率$v$抛出，初速度方向可以任意. 点电荷所受重力可以忽略. 则点电荷到达地面的最短用时为______.
   
8. 一根长度为$l$的轻质刚性杆上端固定一个质量为$M$的质点小球，轻杆初始时竖直立在足够粗糙的地面上，杆与地面接触点为O，如图所示. 现给杆一个扰动，使其倾倒，则小球落地点与O相距______.
   

三. 解答题

9. 如图所示，一薄凸透镜焦距为 $ f $ ，一平面镜MN与其光轴的夹角为 $ 45^{\circ} $ ，且N点在距薄凸透镜光心 $ 2f $ 处，现在以光心为坐标原点，光轴为 $ x $ 轴，水平向右为 $ x $ 轴正方向，竖直向上为 $ y $ 轴正方向建立平面直角坐标系.
   
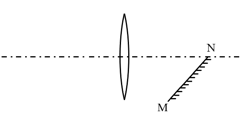
   1. 若从凸透镜左侧入射一束平行光，试求被MN反射后所成像的点的坐标. (2分)
   2. 若在左侧距光心 $ 2f $ 处有一根正置的小蜡烛，烛焰可以视为点光源，到光轴的距离为 $ h(h\ll f) $ ，试求其发出的光在通过凸透镜并被MN反射所呈像的点的坐标. (4分)
   3. 若在左侧距光心 $ 2f $ 处有一根倒置的小蜡烛，烛焰可以视为点光源，到光轴的距离为 $ h(h\ll f) $ ，试求其发出的光在通过凸透镜并被MN反射，并再次反向通过凸透镜后所呈像的点的坐标. (4分)
10. 1827年，R. 布朗观察到了花粉颗粒在水中的无规则运动，于是流体中悬浮微粒的无规则运动被称为布朗运动，后来爱因斯坦对这个问题进行了研究. 考虑三维空间中花粉颗粒的布朗运动，在初始时刻以它所在的位置为原点建立坐标系，那么我们可以计算在之后的 $ t $ 时刻，这颗花粉离原点距离的平方的统计平均值：\[\overline{r^2}=6Dt\]其中 $ D $ 称为扩散系数，与微粒、液体、温度均有关系，爱因斯坦关系式是有关扩散系数 $ D $ 的公式：\[D=\frac{T}{6\pi R\eta}\]其中 $ R $ 为花粉半 径， $ \eta $ 为液体的黏度，与液体性质有关， $ T $ 为液体温度，本题中令玻尔兹曼常数为1.
    1. 试阐述花粉发生布朗运动的原因，并定性地说明为什么扩散系数 $ D $ 会与温度 $ T $ 正相关，为什么会与花粉半径 $ R $ 负相关. (5分)
    2. 某花粉微粒尺寸约 $ b $ ，在黏度为 $ \eta $ ，温度为 $ T $ 的液体中做布朗运动，试计算它在液体中游走距离数量级为 $ b $ 所需要时间的数量级. (5分)
    3. 考虑一种模型，其中假设花粉微粒是朝某个确定方向以某个随机的速度大小游走，即在游走过程中速度大小可以随机改变，速度大小的统计平均值是 $ v $ ，那么花粉在 $ t $ 时刻与原点的距离的平均值就应该是 $ |r| = vt $ ，那么距离平方的平均值就是 $ \overline{r^2}=v^2t^2 $ ，与时间的平方成正比，与 $ \overline{r^2} = 6Dt $ 不同. 有人认为从直觉上，这 两种模型本应等价. 而皮兰的实验证实，用后者描述布朗运动是正确的. 试对前者不能描述布朗运动的原因进行阐释. (5分)
11. 1911年，H. 卡末林·昂内斯发现了某些金属在低温下电阻为0，这些电阻为0的特殊导体被称为超导体，1933年，实验发现超导体内部能够完全排除外磁场，称为超导体的迈斯纳效应. F. 伦敦与H. 伦敦提出的伦敦方程一定程度上可以唯象地解释迈斯纳效应：\[\nabla \times \vec{J}=-\frac{n_s e^2}{m} \vec{B}\]其中 $ n_s $ 是单位体积超导电子数， $ m $ 为电子质量， $ e(e< 0) $ 为电子电荷量， $ \vec{J} $ 是超导电流密度. 将伦敦方程与麦克斯韦方程结合，可以得到超导体内的磁感应强度分布为：\[\vec{B}=\vec{B}_0 \mathrm{e}^{-x / \delta}\]$ \vec{B}_0 $ 是超导体表面的磁感应强度，平行于超导体表面， $ \delta=\sqrt{m/(\mu_0n_se^2)} $ ，一般而言是个很小的常数， $ \mu_0 $ 是真空磁导率. 因此磁感应强度随着深度增加而指数减小，于是在进入超导体的过程中磁场很快就趋近于0，这解释了迈斯纳效应.
    1. 试简要阐述超导体的特征. (2分)

    · 要解释更多超导体的特性，可以使用BCS模型. 该模 型是说，当温度很低时，电子间的库仑排斥力小于由于交换虚声子而产生的吸引力，于是电子会形成库珀对，成为超流凝聚体，这种超流凝聚体可以无能耗地运动. 而描述这种凝聚体需要用“宏观波函数”描述，宏观波函数 $ \mu $ 为：\[\mu=\sqrt{\frac{n_s}{2}}\mathrm{e}^{\mathrm{i}\phi}\]其中 $ \phi $ 是波函数的相位. 我们给出外磁场的矢势 $ \vec{A} $ 与超导电流密度、 $ \vec{J} $ 所满足的规范不变的关系式：\[\vec{J}=\frac{\hbar e n_{{s}}}{2 m}\left(\nabla \phi-\frac{2 e}{\hbar} \vec{A}\right)\]其中 $ \hbar $ 是约化普朗克常数.

    2. 考虑在磁场强度大小为 $ H $ 的外磁场中放一个半径为 $ R $ 的超导小球，且 $ R \ll \delta $ ，并且为简单起见取波函数的相位 $ \phi = 0 $ ，该超导小球的穿透深度 $ \delta $ 已知. 试求该小球的磁化率 $ \chi_m $ . (12分)

    · 超导体的超导性会在磁场过大，或者温度过高时被完全破坏. 通过二级相变理论，可以计算超导体的临界的磁场强度 $ H_c $ 与临界温度 $ T_c $ . 在 $ T_c $ 附近，凝聚体变得很少，所以波函数也极小，在 $ T_c $ 的左邻域内，将体积为 $ V $ 的超导体的亥姆霍兹自由能 $ F $ 按波函数 $ \mu $ 展开，由于对称性，只有偶数次幂：\[F=F_n+a V|\mu|^2+\frac{b V}{2}|\mu|^4\]其 中 $ F_n $ 是临界温度的自由能， $ b $ 是常数， $ a $ 正比于 $ \left(T_c-T\right) $ . 当温度小于 $ T_c $ ，超导体自由能极小的条件给出：\[|\mu|^2=-\frac{a}{b}=\frac{\alpha}{b}\left(T_c-T\right)\]于是可以计算出临界磁场与临界温度的关系：\[H_c=\left(\frac{4 \pi \alpha^2}{b}\right)^{1 / 2}\left(T_c-T\right)\]结合规范不变的超导电流密度表达式，可以导出超导电流密度 $ \vec{J} $ 与波函数 $ \mu $ 的关系.

    3. 选择下列(i)或(ii)其中的一种情况，配合麦克斯韦方程组，计算在相同的温度下它们的临界磁场强度值与大尺度超导体的临界磁场强度值的比值. 相应的超导体的穿透深度 $ \delta $ 已知.
       (i) 厚度为 $ d\ll\delta $ 的平面薄膜超导体，磁场方向平行于薄膜.
       (ii) 半径为 $ R \ll \delta $ 的超导小球.
       *注意：应当注意一个近似，即(i)中沿薄膜厚度方向的 $ \mu $ 和(ii)中的小球内部的 $ \mu $ 都可视作常数. (21分)

第一届OPhO参考答案

1. B
2. C
3. A
4. D
5. \[1-\frac{T_1}{T_2}\]
6. \[\frac{1}{n}\left(\frac{1-n^2\sin^2\theta}{1-\sin^2\theta}\right)^{3/2}\]
7. \[\frac{m}{qB}\arcsin\left(\frac{qBh}{mv}\right)\]
8. \[4\left(\frac{\sqrt{23}-\sqrt{5}}{27}\right)L+\frac{\sqrt{5}}{3}L\]
9. 1. \[(2f,-f)\]
   2. \[(2f-h,0)\]
   3. \[\left(-\frac{f+h}{2f^2+fh},0\right)\]
10. 1. 分子热运动导致水分子撞击花粉方向具有随机性；温度越高，分子热运动越剧烈；花粉越小，撞击不均匀的可能性越大.
    2. \[\frac{\eta b^3}{T}\]
    3. 前者的模型是一种定向的机械运动，没有计及往回走的可能性，而布朗运动是一种随机的往复运动.
11. 1. 超导体电阻为0；在一定温度范围内外界施加一定强度范围的磁场，磁场不会透入超导体内部.
    2. \[\chi_m=-\frac{R^2}{40\delta^2}\]
    3. (i)\[2\sqrt{6}\frac{\delta}{d}\](ii)\[2\sqrt{5}\frac{\delta}{R}\]