线上物理竞赛 Online Physics Olympiad

第十一届OPhO决赛试题

解答题：从下列四道选题中任选两道作答，每道题75分，多做的部分不给分

1. 某人在自己的电脑上存储了一份非常重要的文件，他时不时就打开该文件查看一下，生怕由于存储文件的硬件出了故障导致文件内容发生了变化. 一个很有趣的问题是：该文件是否会因为该人查看的次数比较多而被保存得更好？换句话说，是否会因为该人多次查看该文件，该文件的存储就更不容易出错了？假设此人使用的是经典计算机，我们几乎无需怀疑，答案是否定的；然而，如果此人使用的是量子计算机，情况可能就不那么简单了.

   · 我们将先分析芝诺悖论. 自古以来，人们就曾思考过观测是否会对物理事实造成影响的问题. 有人考虑了如下赛跑问题：A与B在一条直跑道上跑步，初始时A在B前方距B为 $ L_1 $ 的远处以速率 $ v_1 $ 做匀速直线运动，B则以速率 $ v_2 (v_2 > v_1) $ 追赶A.

   1. 试计算B追赶上A所需的时间. (1分)
   2. 对于上述赛跑问题，如果换一种角度来看，B似乎永远也追赶不上A. 因为起初B需要先跑长度 $ L_1 $ 以到达初始时A所在的位置（记为第 1 次追赶），可是当B到那里后，A又向前跑了一段距离，记此时A在B前方 $ L_2 $ 处，于是B要想追上A就需要再向前跑 $ L_2 $ （记为第2次追赶），可是当B向前跑了 $ L_2 $ 后，A又到达了B前方 $ L_3 $ 处……这样下去，B永远也 追不上A. 试基于上述逻辑计算从开始到B完成第 $ n $ 次追赶所需的时间. (2分)
   3. 对于(2)中结果，试证明在 $ n\rightarrow +\infty $ 下与(1)中结果一致. (3分)
   4. 在上述赛跑问题中，如果频繁检查B的位置（即分立地看 $ n $ 次A追B的过程），就会陷入上述逻辑循环，得出B永远也追不上A的荒谬结论，这似乎表明了是否进行观测将导致不同的物理事实——如果不观测，B就能追上A，如果频繁地观测，B就不能追上A. 请给出对上述悖论的解释，并结合此解释谈谈你对数学和物理之间的关系的理解. (8分)

   · 不同于经典世界，量子世界的测量通常会不可避免地影响到系统的状态. 量子理论中，任何粒子都有一个称为自旋的内禀自由度，一个自旋为 $ {1}/{2} $ 的粒子的自旋有可能处于沿空间某轴“向上”或“向下”两种本征状态，亦或处于两种本征状态的叠加状态. 例如，粒子自旋可以处于状态：\[|\Psi\rangle=c_1|+x\rangle+c_2|-x\rangle\]其中 $ |+x\rangle $ 、 $ |-x\rangle $ 分别表示自旋沿 $ x $ 轴正方向和负方向的本征状态，粒子处在状态 $ |\Psi\rangle $ 就是处在这两个状态的叠加 态. 当测量粒子沿 $ x $ 轴的自旋时，有 $ |c_1|^2 $ 的几率测得结果是自旋沿 $ x $ 轴向上，有 $ |c_2|^2 $ 的几率测得结果是自旋沿 $ x $ 轴向下（ $ |c_1|^2+|c_2|^2=1 $ ）. 另外，自旋沿 $ x $ 轴的两种本征状态又可以由沿 $ z $ 轴正方向和负方向的本征状态 $ |+z\rangle $ 、 $ |-z\rangle $ 表示为：\[|+x\rangle=\frac{1}{\sqrt{2}}\left(|+z\rangle+|-z\rangle\right),\qquad |-x\rangle=\frac{1}{\sqrt{2}}\left(|+z\rangle-|-z\rangle\right)\]

   5. 考虑上述状态 $ |\Psi\rangle $ 中， $ c_1=c_2=1/\sqrt{2} $ 的情况，并测量粒子沿 $ z $ 方 向的自旋. 一种观点认为，将以上 $ |+x\rangle $ 、 $ |-x\rangle $ 的表示式代入 $ |\Psi\rangle $ 的表示式中，将得到 $ |\Psi\rangle=|+z\rangle $ ，即测量必将得到自旋沿 $ z $ 轴正方向的结论；另一种观点认为，粒子处于 $ | + x\rangle $ 和 $ | − x\rangle $ 的叠加态，而 $ | + x\rangle $ 、 $ | − x\rangle $ 又都是由 $ | + z\rangle $ 和 $ | − z\rangle $ 两个态叠加形成的，因此测量 $ |\Psi\rangle $ 有1/2的几率得到 $ | + x\rangle $ ，也有1/2的几率得到 $ |− x\rangle $ ，无论得到哪个，此后都 各有1/2的几率得到 $ | + z\rangle $ 和 $ | − z\rangle $ ，因此测量粒子 $ z $ 方向的自旋将有1/2的几率得到自旋沿 $ z $ 轴正方向，有1/2的几率得到自旋沿 $ z $ 轴负方向. 试分析上述两个观点的正误，并阐释理由. (8分)

   · 在量子力学中，量子系统的状态 $ |\Psi(t)\rangle $ 随的时间 $ t $ 的演化可以由薛定谔方程描述. 如果一个量子系统初始 $ t=0 $ 时刻处于状态 $ |\Psi(0)\rangle $ ，则在某 $ t >0 $ 时刻发现系统仍处在初始状态 $ |\Psi(0)\rangle $ 的概率 $ P(t) $ 可根据薛定谔方程计算出. 可以证明，量子系统初始 $ t=0 $ 时发生衰变（量子态发生改变）的速 率为0，即一定有：\[\lim _{t \rightarrow 0} \frac{\mathrm{d} P(t)}{\mathrm{d} t}=0\]

   6. 考虑由 $ N $ 个同种放射性粒子构成的系统，其衰变速度（单位时间内发生衰变的粒子数）正比于 $ N $ ，比例系数为 $ \lambda $ ，试求该放射性粒子的衰变概率随时间变化的表达式，并分析计算结果与上述提到的结论“量子系统初始时发生衰变的速率为0”是否矛盾. (10分)
   7. 在上述情景中若在时间 $ (0, t) $ 内对该量子系统进行 $ N $ 次对该物理量的测量，相邻两次测 量的间隔时间相等，并假设测量可以瞬间完成，试求 $ N\rightarrow\infty $ 的情况下 $ t $ 时刻系统仍处于初状态 $ |\Psi(0)\rangle $ 的概率. (10分)

   · 在量子信息中，用于编码数据的基本信息单位称为量子比特. 一个量子比特可以处于状态 $ |0\rangle $ 、 $ |1\rangle $ ，或两种状态的叠加态. 利用量子比特可以实现计算或信息传递. 在量子计算机中，常常使用冗余码来存 储量子信息，如使用3个量子比特来存储 $ |0\rangle $ 和 $ |1\rangle $ ：\[|0\rangle=|0\rangle_1|0\rangle_2|0\rangle_3, \qquad|1\rangle=|1\rangle_1|1\rangle_2|1\rangle_3\]如果一段时间后发现3个量子比特中有1个和其他2个不同，则自动调整那个不同的量子比特，从而完成纠错.

   8. 若 $ t = 0 $ 时存储的所有量子信息都是正确的，假设单一量子比特在一段时间 $ t $ 后出错的概率为 $ q(t) $ . 试计算 $ t $ 时刻使用上述方法纠错后量子信息仍保持正确的概率，并探讨当 $ q(t) $ 满足什么条件时，使用上述 纠错方案相比于不使用（即不使用冗余码，而是直接存储量子信息）更有优势. (11分)
   9. 对于(8)中存储量子信息的问题，试证明：在使用冗余码后，如果时常观测量子信息，将降低该信息 存储出错的概率. 从而说明，如果某人使用的是量子计算机，那么时常观测已存储的信息确实可以使信息被保存得更好. (11分)
   10. 对于(8)中存储量子信息的问题，实践表明，某人时常观测信息确实降低了信息存储出错的概率，但当其观测过于频繁时，反而发现信息出错的概率提高了，试阐释发生这种现象的原因. (11分)
2. 一个密绕螺线管可以作为一个电感器件接入电路，通常，人们在这样的电感器件中填充各种磁介质，在不影响电感器件的几何尺寸的情况下，来改变其电感数值. 在本题中，你将会看到，如果将磁介质更换为导体，那么这种电感元件会成为一种测量材料电导率的技术，其最有价值的特征在于，这种测量对材料样品是非接触式的. 考虑一个线密度为 $ n $ ，总长度为 $ l $ ，截面为圆形，面积为 $ S=\pi a^2 $ 的密绕螺线管，内部为真空，线圈材料的电阻忽略不计. 忽略边缘效应，忽略线圈对外的辐射，即假设螺线 管外部不存在电磁场，长度 $ l $ 远远大于任何出现的其他长度尺度. 真空磁导率为 $ \mu_0 $ .
   1. 如果线圈通有稳恒电流 $ I $ ，试求螺线管内部的磁感应强度大小. (3分)
   2. 试求该螺线管产生自感的自感系数. (3分)
   3. 如果将该螺线管与一简谐交流电源相接，试说明电路的伏安特性和能量转化. (6分)

   · 如果在该螺线管内填充电导率为 $ \sigma $ 的导体材料，其相对磁导率为1，导体材料同螺线管绝缘. 此时将电感器件接入圆频率为 $ \omega $ 的简谐交流电，导体会出现电流，称为傅科电流或涡流. 这种涡流的热效应是测量的核心.

   4. 为具体计算导体材料对电路的影响，共需要4个参数，试说明除了交流电圆频率 $ \omega $ 、电导 率 $ \sigma $ 、真空磁导率 $ \mu_0 $ 之外，剩下一个需要的参数是什么. (6分)
   5. 对(4)中的4个参数在国际单位制中展开量纲分析，构造一个无量纲参数 $ \xi $ . 当导体的存在对 电路的影响足够小时，应当有 $ \xi\ll 1 $ . (7分)
   6. 试求该螺线管内部导体中的涡流耗散功率，精确到 $ \xi $ 的一阶. (10分)
   7. 螺线管内导体的涡流耗散的存在使得该电路等效为理想电感和一个满足欧姆定律的电阻器的串联，试求该等效电阻，精确到 $ \xi $ 的一阶. (10分)
   8. 从能量的角度来看，螺线管内导体的涡流耗散等效为串接电阻. 但在电路的角度这并不直观——导体并不参与到闭合回路中. 试从螺线管线圈中出现的反电动势的角度解释电路中为什么会产生这样的耗散，并求出这个反电动势，证明(7)中 通过能量转化角度给出的等效电阻在 $ \xi $ 的一阶是正确的. (13分)
   9. 考虑相反的极限，例如交流电的频率足够大，使 $ 1/\xi\ll 1 $ （但仍有 $ \omega a\ll c $ ） ，此时螺线管中导体内的磁场和涡流将趋向于分布在导体表面，该现象称为趋肤效应. 在该情况下，试在 $ 1/\xi $ 的最低阶求出等效电阻. (17分)
3. 在物理学中，某些系统的演化非常敏感地依赖于初始条件，即初始条件的细微变化，会导致系统后续的解在状态空间上的显著差异，通俗地说，初始条件的微小变化，会带来差异巨大的物理结果，这种现象被称为蝴蝶效应. 蝴蝶效应通常发生 在具有非线性特征的混沌系统中，十九世纪六十年代，詹姆斯·麦克斯韦首先强调了蝴蝶效应，被认为是最早研究混沌理论的. 本题我们探讨经典力学中一种最简单的混沌系统.
   考虑单个质点在一个有界二维平面上的运动. 在平面内部运动时，质点不受任何力， 当质点与边界碰撞反弹时，遵循“入射角等于反射角”的规律，质点的速率始终恒定. 初始时质点从平面内的某位置朝某方向发射，之后平面内无疑会有一条质点的运动轨迹，我们现在考察对质点的初始条件进行微小改变后轨迹的变化，初始条件的变化可以分解为两种“基变 化”，如图所示，质点在初始时刻过后的轨迹本为A，我们可以稍微改变质点初始的速度方向，使初始后瞬间的轨迹B与A有一很小夹角 $ \varphi_0 $ ；另外，我们可以保持初始速度方向不变，但是在垂直于速度方向上移动质点的初始位置一个微小的距离 $ r_0 $ ，使初始时刻后的轨迹变为C（沿速度方向上的平移是平凡的）；而一般的初始条件变更可以是以上两种变化的组合. $ \varphi_0,r_0 $ 左移/左旋转时取正值，右移/右旋转时取负值，. 在经过一段时间 $ t $ 后，对初始条件进行变更后的质点轨迹相较于原轨迹的区别，也可以分解为速度方向的夹角 $ \varphi(t) $ ，和垂直于原轨迹速度方向上的位置分离 $ r(t) $ . 在本题所有小问中均使用上述记号且 $ \varphi_0\ll 1 $ ，质点速率恒为 $ v $ .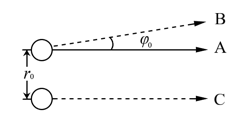
   
   1. 若质点的初始位置离边界足够远，即质点不反弹故轨迹一直是直线，对初始条件进行的变更为 $ \varphi_0 $ 与 $ r_0 $ ，试求 $ \varphi(t) $ 与 $ r(t) $ . (2分)
   2. 若质点仅与直线型边界碰撞反射了一次，对初始条件进行的变更为 $ \varphi_0 $ 与 $ r_0 $ ，试求 $ \varphi(t) $ 与 $ r(t) $ . (4分)
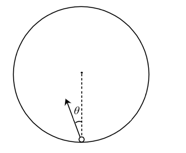
   3. 考虑质点所运动的有界二维平面是一个半径为 $ R $ 的圆的内部，初始时质点在边界上，初始速度 与其与圆心连线的夹角为 $ \theta $ ，如图所示. 若对初始条件进行的变更为 $ \varphi_0 $ 与 $ r_0(r_0\ll R) $ ，试求质点与边界碰撞反射一次后的 $ \varphi(t) $ 与 $ r(t) $ . (6分)
      

   · 我们可以根据 $ \varphi(t) $ 与 $ r(t) $ 在足够长的时间下是否快速增长来判断一个系统是否是初值敏感的. 对于一个系统，在演化足够长时间后，若 $ \varphi(t) $ 与 $ r(t) $ 只对极个别特殊的 $ \varphi_0 $ 与 $ r_0 $ 不增长，而对其它微小的初值变更都使 $ \varphi(t) $ 和/或 $ r(t) $ 指数型增长，则系统就是初值敏感的混沌系统. 在 $ t\rightarrow \infty $ 时，对混沌系统一般有 $ \varphi(t)\propto \exp(\lambda_1 t) $ 和/或 $ r(t)\propto \exp(\lambda_2 t) $ ，其中 $ \lambda_1 >0,\lambda_2 >0 $ 称为李雅普诺夫指数.

   4. 考虑质点所运动的有界二维平面是一个矩形的内部，质点的运动是否是初值敏感的？试证明你的结论. (12分)
   5. 在(3)的条件下，试求质点与边界碰撞反射 $ n $ 次后的 $ \varphi(t) $ 与 $ r(t) $ ，并据此指出该种圆形边界是否属于初值敏感的混沌系统. (15分)
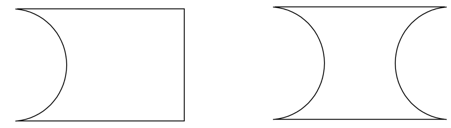
   6. 考虑如图左图所示的有界二维平面. 即将矩形平面的一条边替换为一个向内凹陷的半圆作为边界. 对该系统，质点的运动是否是初值敏感的？若如右图将矩形的两条对边分别替换为向内凹陷的半圆呢？试证明你的结论. (18分)
      
   7. 对本题的情景，即有界二维平面内的质点在内部自由运动，反弹时“入射角等于反射角”，若系统是混沌的，证明李雅普诺夫指数有 $ \lambda_1=\lambda_2 $ . (18分)
4. 常见的热力学系统可以用各个参量来表示其状态，例如粒子数 $ N $ ，温度 $ T $ ，体积 $ V $ 等. 不失一般 性，我们可以设对一个系统的微小的输入功 $ \mathrm{d}W $ 可表示为 $ \mathrm{d}W=Y\mathrm{d}y $ ，其中 $ Y $ 是广义力， $ y $ 是对应的广义坐标，例如，如果广义坐标是热力学系统的体积 $ V $ ，则广义力 $ Y $ 就是压强的负值 $ -p $ ，从而得到体积功 $ \mathrm{d}W=-p\mathrm{d}V $ .
   通过热力学系统的熵 $ S $ 和内能 $ U $ 定义的热力学系统的热力学温度 $ T $ 为：\[T=\left(\frac{\partial U}{\partial S}\right)_y\]根据上述定义，存在某些热力学系统，其可以处于负温度状态，即该系统的热力 学温度 $ T< 0 $ .
   1. 写出热力学系统的热力学第一定律的微分形式与热力学第二定律的微分形式. (3分)
   2. 试根据热力学温度的定义分析热力学系统具有负温度状态的必要条件是什么. (4分)
   3. 考虑性质完全相同的两个热力学系统，初始温度分别为 $ T_1,T_2 $ ，且 $ T_1=-T_2 $ ，试求两 个系统的热平衡温度. (5分)
   4. 考虑到负温度系统的特殊性，试通过热力学温度 $ T $ 定义一个尽可能简单的新温标 $ T^*(T) $ ，使得 $ T^* $ 在数值上更大的热力学系统能够自发地向 $ T^* $ 更小的热力学系统传热. (5分)
   5. 考虑一个在温度分别为 $ T_1 $ 与 $ T_2 $ 的两个热源下工作的热机，若 $ T_1< T_2< 0 $ ，试 求该热机的最大的工作效率及相应的循环方式. (7分)

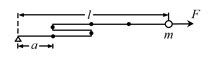
   · 对任一热力学系统，若其微观状态数为 $ \Omega $ ，则其玻尔兹曼熵定义为 $ S=k\ln \Omega $ . 其中 $ k $ 为玻尔兹曼常数. 现考虑一根链条，总长度为 $ L $ ，每段长为 $ a $ ，一端固定，另一端有质量为 $ m $ 的质点，每段的取向只能向左或者向右，例如图中，链条只有一段取向向左，其它段的取向向右. 现在质点上施加沿着链条末段的方向的大小为 $ F $ 的外力. 设 $ L\gg a $ ，且已知质点的位置相对固定端的坐标为 $ l $ （质点位置相对固定端的方向与外力方向相同时 $ l $ 取正 值）.
   

   6. 试求质点在外力势场中的能量 $ U $ 与该系统的总微观状态数 $ \Omega $ . (9分)
   7. 试求该系统的温度 $ T $ 与能量 $ U $ 之间的关系式 $ T(U) $ ，可以利用合理近似，并绘制函数草图（你会发现当 $ U >0 $ 时，该系统处于负温度状态）. (12分)

   · 考虑在体积为 $ V $ 的区域中均匀分布了 $ N $ 个固有电偶极矩为 $ p $ 的电偶极子，假设每个电 偶极子之间无相互作用，在空间中取向任意，现加上外电场 $ E $ ，不计电偶极子自身的热容.

   8. 试求该系统的内能与温度的关系式 $ U(T) $ . (12分)
   9. 若当系统温度处于 $ T=T_0 $ ，外电场 $ E=E_0 $ 时，熵 $ S=S_0 $ . 试求系统的熵关于温度的 关系式 $ S(T) $ ，并指出该系统的内能 $ U $ 在满足何种条件时系统将处于负温度状态. (18分)

第十一届OPhO决赛参考答案

1. 1. \[t=\frac{L_1}{v_2-v_1}\]
   2. \[t_n=\frac{L_1}{v_2} \frac{1-\left(\frac{v_1}{v_2}\right)^n}{1-\frac{v_1}{v_2}}\]
   3. 考虑到 $ v_2 >v_1 $ ，故：\[\lim _{n \rightarrow+\infty} t_n=\lim _{n \rightarrow+\infty} \frac{L_1}{v_2} \frac{1-\left(\frac{v_1}{v_2}\right)^n}{1-\frac{v_1}{v_2}}=\frac{L_1}{v_2-v_1}=t\]证毕.
   4. 略.
   5. 第一种观点是正确的，第二种观点是错误的. 一方面可以直接根据量子力学的基本原理中关于测量的叙述来理解，测量哪个物理量，就要将系统的状态按该物理量所对应的算符的本征态完备组进行展开，因此测量 $ z $ 方向的自旋, 就应该 将 $ |\Psi\rangle $ 按 $ |+z\rangle, |-z\rangle $ 展开，不应再考虑 $ |+x\rangle, |-x\rangle $ . 另一方面可以理解为，量子力学中的叠加是概率幅的叠加，即相干叠加，而不是简单的概率叠加（非相干叠加）， 这是第二种观点错误的主要原因.
   6. \[p(t)=1-\exp(-\lambda t)\]或：\[p(t)=\lambda t\]不矛盾，因为基于薛定谔方程的证明的前提是所有粒子在 $ t=0 $ 时的状态都是一 致的（纯态系综），而这里计算衰变问题时不同粒子的初始状态当然是不同的，两个问题的前提不同，因此并不矛盾.
   7. 1
   8. \[q(t)< \frac{1}{2}\]
   9. 略.
   10. 这是因为，量子力学中有能量和时间的不确定性关系：\[\Delta E \Delta t \geq \frac{\hbar}{2}\]过于频繁的测量会造成系统具有较大的能量不确定度，使系统的涨落更加明显，从而导致信息存储更容易出错.
2. 1. \[B=\mu_0 nI\]
   2. \[L=\mu_0 \pi n^2 la^2\]
   3. \[U(t)=\mathrm{i}\omega LI(t)\]不存在能量耗散，电路中的电势能与磁场能互相转化，在一个周期内 各达到两次峰值.
   4. 线圈半径 $ a $ ，或截面积 $ S $ .
   5. 在MLT系统中对各参数展开量纲分析：\[\begin{aligned}\omega & \sim T^{-1} \\a & \sim L \\\sigma & \sim \frac{M L^2 T^{-3} / L^3}{\left(M L T^{-2} /(I T)\right)^2}=\frac{I^2 T^3}{M L^3} \\\mu_0 & \sim \frac{M L T^{-2}}{I^2}\end{aligned}\]从而可以构造无量纲参量为：\[\xi=\mu_0 \sigma \omega a^2 \]
   6. \[P =\frac{\pi \sigma l a^4 }{16}\left(\omega \mu_0 n I_0\right)^2 \]
   7. \[R=\frac{\pi l a^4 \sigma}{8} \omega^2 \mu_0^2 n^2\]
   8. 略.
   9. \[R=\pi n^2l a\sqrt{\frac{{2\mu_0\omega}}{{ \sigma }}}\]
3. 1. \[r(t)=r_0+vt\varphi_0\]\[\varphi(t)=\varphi_0\]
   2. \[r(t)=-r_0-vt\varphi_0\]\[\varphi(t)=-\varphi_0\]
   3. \[r(t)=3r_0-(3vt-8R\cos\theta)\varphi_0\]\[\varphi(t)=\frac{2r_0}{R\cos\theta}+\left(\frac{2vt}{R\cos\theta}-5\right)\varphi_0\]
   4. 矩形边界并不初值敏感，证明略.
   5. \[r(t)=(1-2n)r_0-2nR\varphi_0\cos\theta\]\[\varphi(t)=\frac{2n r_0}{R\cos\theta}+(2n+1)\varphi_0\]圆形边界并不初值敏感.
   6. 两种边界均初值敏感，证明略.
   7. 略.
4. 1. 热力学第一定律：\[\mathrm{d} U=\mathrm{d} Q+Y \mathrm{d} y \]热力学第二定律：\[\mathrm{d} S \geq \frac{\mathrm{d} Q}{T}\]
   2. 热力学系统要存在负温度状态，内能至少要有（局部的）极值，或者说熵和内能的关系不能是单调的.
   3. 二者的热平衡热力学温度为：\[T \rightarrow \infty\]
   4. \[T^*=-\frac{1}{T}\]
   5. \[\eta=1-\frac{T_2}{T_1}\]
   6. \[U=-Fl\]\[\Omega=\frac{\left(\frac{L}{a}\right)!}{\left(\frac{L+l}{2 a}\right)!\left(\frac{L-l}{2 a}\right)!}\]
   7. \[T=\frac{2 a F}{k \ln \frac{L F-U}{L F+U}}\]当 $ U< 0 $ 时，温度 $ T >0 $ 并从+0单调增至 $ +\infty $ ，当 $ U >0 $ 时，温度 $ T< 0 $ 并从 $ -\infty $ 单调增加至-0.
   8. \[U(T)={NkT}-N p E \operatorname{coth}\left(\frac{pE}{kT}\right)\]
   9. \[S=S_0+N k\left[\ln \left(\frac{ T}{e T_0} \frac{E_0}{E} \frac{\sinh \left( \frac{p E}{kT}\right)}{\sinh \left(\frac{p E_0}{k T_0}\right)}\right)+\frac{pE}{kT} \operatorname{coth}\left(\frac{pE}{kT}\right)\right]\]