线上物理竞赛 Online Physics Olympiad

第十届OPhO预赛试题

单选题：在每道题的4个选项中，有且仅有1个选项是符合题意的，第1-10题每题5分，第11-20题每题10分

1. 十七世纪物理学家艾萨克·牛顿在他的著作《自然哲学的数学原理》中提出：“物体会保持其静止或匀速直线运动状态，除非有外力迫使其改变这种状态.”该物理定律被称为______.
   1. 牛顿第一定律
   2. 牛顿第二定律
   3. 牛顿第三定律
   4. 万有引力定律
2. 一个质地均匀的球体，质量为 $m$ ，密度为 $\rho$ ，则它的半径为______.
   1. $\sqrt[3]{\frac{4\pi \rho}{3m}}$
   2. $\sqrt[3]{\frac{4\pi m}{3\rho}}$
   3. $\sqrt[3]{\frac{3\rho}{4\pi m}}$
   4. $\sqrt[3]{\frac{3m}{4\pi \rho}}$
3. 单个原子的尺度的数量级为______.
   1. $10^{-10}\mathrm{m}$
   2. $10^{-9}\mathrm{m}$
   3. $10^{-8}\mathrm{m}$
   4. $10^{-7}\mathrm{m}$
4. 当形成闭合回路的导体的一部分在磁场中做切割磁感线的运动时，导体回路中会产生电流，这种现象被称为电磁感应，利用这种原理，可以制作______.
   1. 马达
   2. 电动机
   3. 发电机
   4. 感应起电机
5. 对于一个孤立的、与外界没有相互作用的系统，下列说法不正确的是______.
   1. 系统的总动量一定是守恒的
   2. 系统的总角动量一定是守恒的
   3. 系统内各个部分的机械能总和一定是守恒的
   4. 系统内各个部分的电荷量总和一定是守恒的
6. 如果定义一个单位制，在该单位制中规定真空光速 $c=1$ ，即真空光速没有单位且数值为1，则在该单位制中，下列各量的单位与“质量”的单位一样的是______.
   1. 密度 $\rho$
   2. 能量 $E$
   3. 重力加速度 $g$
   4. 牛顿引力常数 $G$
7. 空调制热与电暖器不同，电暖器直接将电能转化为热能，而空调则是从室外吸热并在室内放出，这个过程需要消耗电能，该部分电能最终同样转化为热，空调搬运的热量与所需电能之比称为制热系数. 如果某台空调的制热系数为 $w$ ，近似可视为常数，在使室内升高相同的温度的情况下（室内空气比热容视为常数），仅使用空调完成和仅使用电暖器完成（电阻丝的热容可忽略不计），所消耗的电能之比为______.
   1. $w$
   2. $w-1$
   3. $\frac{1}{w}$
   4. $\frac{1}{1+w}$
8. 飞行器是能够脱离地面持续飞行的器械，下列有关各种飞行器的说法，不正确的是______.
   1. 飞艇与热气球能够稳定地在空中飞行，是因为其内部通常填充有密度小于空气的气体，从而在空中受到足够大的空气浮力与重力相平衡. 对于同一个飞艇或热气球，它的飞行高度越高时，由于空气密度越低，因此它受到的浮力通常越小
   2. 当空气流过喷气式飞机的机翼时能够产生向上的升力从而稳定飞行，这利用了空气流速较快的地方压力较小的原理，喷壶之所以能喷水，也同样利用了该原理
   3. 离子飞机是指由气体放电产生离子风来作为动力的飞机. 当气体放电时，带电正离子在电场力的驱动下定向运动到飞机后方聚积正电荷的翼面上，离子在运动过程中与空气分子发生碰撞，使空气流动产生对机身的推力
   4. 火箭燃烧室里产生高温高压气体通过喷嘴加速，排出到外界，推动火箭飞行，由于该过程无需外界空气辅助，火箭可以在大气层外飞行; 当载运飞船的火箭的速度达到第一宇宙速度时，飞船可以在近地面围绕地球做圆周运动
9. 如图所示，两面平面反射镜AB和AC交于A，两平面镜的夹角为 $60^\circ$ .在AB和AC的角平分线上放一点光源S， 使光源发出的光在经过平面镜反射后呈像，像的数目是______.
   
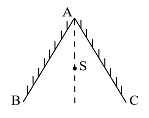
   1. 3
   2. 6
   3. 12
   4. 无穷多个
10. 如图所示，将一斜面A固定在墙角处的水平地面上，在斜面上面放一物体B，物体B恰好可以匀速下滑. 物体B的右侧固定有一水平的轻弹簧，当物体B下滑到靠近墙壁时，墙壁与物体B间的弹簧被压缩，在弹簧逐渐压缩的过程中，地面对斜面的水平作用力的方向是______.
    
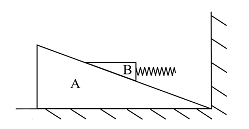
    1. 向左
    2. 向右
    3. 没有水平作用力
    4. 无法判断
11. 从地面竖直向上持续发射一束频率为 $ν_0$ 的光，假设重力加速度为 $g$ ，真空中的光速为 $c$ ，普朗克常数为 $h$ ，不考虑空气的作用，下列说法中正确的是______.
    1. 光从地面向上传播 $x$ 高度后，单光子的重力势能增加了 $h\nu_0 gx/c^2$
    2. 光从地面向上传播 $x$ 高度后，光的频率将减小，减小的多少与 $g$ 有关
    3. 光从地面向上传播 $x$ 高度后，单光子的速度变为 $\sqrt{c^2-2gx}$
    4. 在光的传播路径上，距地面 $x$ 高度处的光子数密度是地面处光子数密度的 $\exp{(-gx/c^2)}$ 倍
12. 现有四个完全相同的体积恒定的绝热气缸置于真空环境中，相隔足够远，现在给四个气缸内部充入同种理想气体，四缸气体的温度满足关系式 $T_1=T_2 > T_3=T_4$ ， 压强满足关系式 $ p_1=p_3 < p_2=p_4$ .现同时在四个气缸的容器壁上开一同样 面积的小圆孔，使得气体分子可以从小孔中泄流而出，则一段时间后，四缸气体的温度变化量的绝对值满足______.
    1. $|\Delta T_2|>|\Delta T_4|>|\Delta T_1|>|\Delta T_3|$
    2. $|\Delta T_2|>|\Delta T_1|>|\Delta T_4|>|\Delta T_3|$
    3. $|\Delta T_1|=|\Delta T_2|>|\Delta T_3|=|\Delta T_4|$
    4. 无法确定
13. 一辆高铁内坐有一人，他面前的桌上放有一个长、宽、高分别为 $l$ 、 $w$ 、 $h$ 的长方体形的盛有水的杯子 ，杯子的宽边所在的方向恰好与高铁前进的方向平行，假设高铁沿水平方向直线行驶，杯子的底面始终水平，人面朝的方向和高铁行驶的方向相同，杯子与人均与高铁保持相对静止，不计水的表面张力，水可以看作密度为 $\rho$ 且均匀分布的液体，重力加速度大小为 $g$ ，下列说法正确的是______.
    1. 如果高铁由匀速行驶突然变成了加速行驶，那么杯中的水有可能溅到人的身上
    2. 如果高铁匀速行驶，此时杯中装满了水，某时刻起高铁开始缓慢地加速行驶，加速度大小由 $0$ 缓慢增 大到 $a$，稳定后，从杯中溢出的水的质量约为 $a\rho lw^2/2g$
    3. 如果高铁匀速行驶，此时杯中装满了水，某时刻起高铁开始缓慢地加速行驶，加速度大小由 $0$ 缓慢增 大到 $a$ ，稳定后，此人感觉自己和座位之间的压力比高铁匀速行驶时大，因此此时杯中水的内部压强的最大值有可能大于高铁匀速行 驶时杯中水的内部压强的最大值，但是如果 $a$ 很大导致水溢出太多的话，此时杯中水的内部压强的最大值也有可能小于高铁匀速行驶 时杯中水的内部压强的最大值
    4. 如果高铁匀速行驶，假想在杯中水的内部取一直角三棱柱形液体区域，三棱柱的三个侧面分别位于水平、竖直、倾斜方向，处于倾斜方向的侧面在处于水平方向的侧面的上方，当这个三棱柱形液体区域的空间尺度趋于 $0$ 时，其竖直侧面的 平均压强小于水平侧面的平均压强
14. 如图所示的俯视图中，一个宽度为 $D$ 的传送带的传送速率为 $v$ ，在传送带其中一边有一个人A在传送带外边 沿传送带的一条边以与传送带相同的速率 $v$ 向右行走，某时刻在传送带另一边的人B发现了传送带对面的人A，此时B与A的直线距离为 $\sqrt{2}D$ ，B于该时刻开始朝人A以 $\sqrt{2}v$ 的速率走去（该速率是相对传送带而言），假设B无时不刻都保持自己面朝着A，则 当B到达传送带另一边时，他与A的距离为______.
    
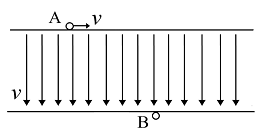
    1. $D$
    2. $ {\sqrt{2}}D$
    3. $ 2({\sqrt{2}-1})D$
    4. $ 4({\sqrt{2}-1})D$
15. 质量为 $m$ 的质点在质量为 $M$ 的固定质点的平方反比引力作用下做轨道运动，运动质点除了机械能与角动量守恒以外，还具有一个守恒矢量，称为拉普拉斯-龙格-楞次矢量（简称LRL矢量），它的定义是： $\vec{A}=\vec{v} \times \vec{L}-GMm \hat{\vec{r}}$ .其中 $\vec{v}$ 是运动质点的速度， $\vec{L}$是运动质点的角动量， $\hat{\vec{r}}$ 是由力心质点指向运动质点的单位矢量， $G$ 是牛顿引力常数，下列说法不正确的是______.
    1. 若运动质点做椭圆轨道运动，则它的LRL矢量垂直于角动量，平行于椭圆的长轴且由焦点指向近心点，如 果轨道是圆，则其LRL矢量为0
    2. 若运动质点做双曲轨道运动，它的LRL矢量大小不一定大于该质点绕此力心做椭圆轨道运动时的LRL矢量大小
    3. 总可选择一个以力心为原点的直角坐标系，使该系中运动质点的角动量的三个分量及LRL矢量的任意一个 分量、机械能作为在平方反比有心力场中运动的质点的5个独立的运动积分，运动质点的任何守恒的运动积分都可以通过这5个独立的运动积分表达
    4. 总可选择一个以力心为原点的直角坐标系，使该系中运动质点的角动量的三个分量和LRL矢量的三个分量 这6个量中任意5个作为在平方反比有心力场中运动的质点的5个独立的运动积分，运动质点的任何守恒的运动积分都可以通过这5个独立的运动积分表达
16. 如图所示，在一波长为 $\lambda$ 的单色相干点光源S前方放一截去一半的薄凸透镜L，S恰好处于L的焦点，M是一平行于轴线的平面反射镜，其到轴线的距离为 $d$ ，在右侧垂直于轴线放一光屏，光屏到S的距离为 $D$ ，$D$ 远大于 $d$ 及透镜焦距. 光屏上干涉条纹的形状为______；如果此时光屏与轴线相交处恰为亮纹，则第一条暗纹到轴线的距离为______.
    
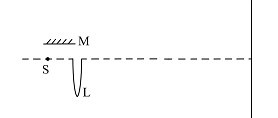
    1. 直条纹；${\sqrt{4d^2+\lambda D}}$
    2. 直条纹；${2d+\sqrt{4d^2+\lambda D}}$
    3. 圆环条纹；${\sqrt{4d^2+\lambda D}}$
    4. 圆环条纹；${2d+\sqrt{4d^2+\lambda D}}$
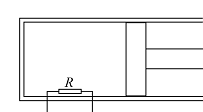
17. 如图所示是一带活塞的密闭绝热容器， $R$ 是一个恒温器，当它开启时，可以使容器内的气体保持当前温度. 现 在容器中充入单原子理想气体，恒温器可以随时开启或关闭，若气体推动活塞膨胀至体积扩大为原来的四倍，温度降为原来的一半，控制恒温器的开关使上述过程中气体对活塞做功达到最大可能值，假设活塞的移动足够缓慢从而气体时刻都处于平衡态，则该过程气体吸收热量与对活塞做功的比值为______.
    
    1. $\frac{\ln 2}{2+\ln 2}$
    2. $\frac{\ln 2}{3+\ln 2}$
    3. $\frac{2\ln 2}{2+2\ln 2}$
    4. $\frac{2\ln 2}{3+2\ln 2}$
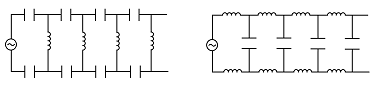
18. 如图所示是两种不同的由电容与电感构成的无穷网络电路，若交流电源的圆频率为 $\omega$ ，已知所有电容器的电容均为 $C$ ，所有电感器的电感均为 $L$ .对于无穷电容电感网络，忽略电磁波辐射. 只有 $\omega$ 满足一定的范围，振荡电流才 能够传到右端的无穷远处（即不会发生衰减），则对图中左与右的两种电路，电流能够无衰减地在电路中向右传播下去的 $\omega$ 的取值范围分别为______和______.
    
    1. $\left[\sqrt{\frac{1}{4LC}},\sqrt{\frac{4}{LC}}\right];\quad \varnothing$
    2. $\left[\sqrt{\frac{1}{2LC}},+\infty\right);\quad \left[\sqrt{\frac{2}{LC}},+\infty\right)$
    3. $\left[0,+\infty\right);\quad \left[\sqrt{\frac{1}{8LC}},\sqrt{\frac{2}{LC}}\right]$
    4. $\left[\sqrt{\frac{1}{4LC}},\sqrt{\frac{4}{LC}}\right];\quad \left[\sqrt{\frac{1}{8LC}},+\infty\right)$
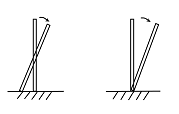
19. 均匀的直细柱静止地立在水平地面上，如细柱在微小扰动下后倾倒，如图所示，考虑两种极限情况：左为地面绝对光滑，右为地面绝对粗糙（最大静摩擦力足够大），重力加速度为 $g$ .试求当细柱与竖直方向夹角为 $\theta$ 时，地面对细柱的支持力大小与细柱重力大小之比在两种情况下分别为______和______.
    
    1. $\frac{4-3\cos\theta+6\cos^2\theta}{(1+3\sin^2\theta)^2};\quad\left(\frac{3\cos\theta-1}{2}\right)^2$
    2. $\frac{4-6\cos\theta+3\cos^2\theta}{(1+3\sin^2\theta)^2};\quad\left(\frac{3\cos\theta-1}{2}\right)^2$
    3. $\frac{4-3\cos\theta+6\cos^2\theta}{(1+3\sin^2\theta)^2};\quad\left(\frac{3\cos\theta-1}{6}\right)^2$
    4. $\frac{4-6\cos\theta+3\cos^2\theta}{(1+3\sin^2\theta)^2};\quad\left(\frac{3\cos\theta-1}{6}\right)^2$
20. 如图所示，真空中水平放置的半无限大接地导体平板边缘的正上方固定有一个点电荷 $q$ ，则导体平板对该点电 荷的力与竖直方向的夹角的正切值为______.
    
    1. $\frac{2}{\pi+2}$
    2. $\frac{2}{\pi-2}$
    3. $\frac{\pi}{\pi+2}$
    4. $\frac{\pi}{\pi-2}$

第十届OPhO预赛参考答案