线上物理竞赛 Online Physics Olympiad

第十届OPhO决赛试题

解答题：从下列四道选题中任选两道作答，每道题75分，多做的部分不给分

1. 由两个折射面包裹一种透明介质构成的光学元件叫做透镜. 为方便透镜的加工和检验，实际生产中一般将 透镜的折射面加工成球面的一部分. 实验表明，靠近透镜主光轴的物体可经透镜成清晰的像. 下面我们将重点研究折射面是球面的透镜在傍轴近似（即光线与主光轴很接近的情况）下的成像特点.
   1. 绝大多数光学元件都无法成清晰的像. 实际上，傍轴光线经透镜所成的像也不是真正清晰的，只是近似清晰而已. 请简要分析像清晰与否取决于什么条件，并举一个能成真正清晰的像的理想光学元件的例子.（4分)
   2. 考虑光线在透镜的一个折射面上的折射，如果折射面两侧介质的折射率分别为 $n_1$ 、$n_2$ ，光 线与法线的夹角分别为 $θ_1$ 、 $θ_2$ ，请写出折射定律的表达式. 如果光线是傍轴的，此时光线与法线的夹角很小，我们知道 $x$ 趋于0时 $\sin x \approx x$，请据此写出傍轴条件下的折射定律的表达式. (4分)
   3. 傍轴条件下的折射定律的形式启发我们，在研究傍轴条件下透镜的成像特点时，空间中任意一点的光线的状态可由两个参数完全描述：一是折射参数 $r = nu$ ，其中 $n$ 表示该点处介质的折射率，$u$ 表示光线与主光轴所夹的锐角， 一般规定如果主光轴旋转一个锐角与光线重合时是顺时针旋转的，那么 $u$ 取正，否则 $u$ 取负；二是位置参数 $d$ ，表示该点到主 光轴的距离，一般规定主光轴一侧的 $d$ 为正，另一侧的 $d$ 为负. 另外，折射面是部分球面的透镜有一个重要的几何参数，就是球面的曲率半径 $R$ ，一般规定主光轴与折射面的交点叫做该折射面的顶点，从顶点指向折射面的球心的向量如果与光线方向所夹的角度为 锐角，则 $R$ 为正，否则 $R$ 为负. 如果一条傍轴光线在透镜的一个折射面上发生折射，折射前瞬间光线的折射参数和位置参数分别为 $r_1$ 、 $d_1$ ，折射面前、后介质的折射率分别为 $n_1$ 、 $n_2$ ，折射面是曲率半径为 $R$ 的球面的一部分，试求折射后瞬间 光线的折射参数 $r_2$ 和位置参数 $d_2$. (12分)
   4. 光在折射率恒定的介质中将沿直线传播. 如果一条折射参数和位置参数分别为 $r_1$ 、 $d_1$ 的傍轴光线在折射率为 $n$ 的介质中传播了一段距离，这段距离沿主光轴方向的长度为 $l$ ，试求传播后光线的折射参数和位置参数 $r_2$ 、 $d_2$ . (12分)
   5. 有一个由若干透镜构成的光学系统，所有透镜的主光轴重合，每个折射面均为部分球面. 在傍轴近似下，如果空间中一点有一条折射参数和位置参数分别为 $r_1$ 、 $d_1$ 的光线，该点经该光学系统所成的像点处的对应光线的折射参数和位置参数 $r_2$ 、 $d_2$ 可一般地表示为：\[r_2=a_1 r_1+a_2 d_1, \qquad d_2=a_3 r_1+a_4 d_1\]其中 $a_1$ 、 $a_2$ 、 $a_3$ 、 $a_4$ 为只与该点位置和该光学系统的性质有关的常数，证明：$a_1a_4 = 1$ .(12分)
   6. 考虑一个真空场景，建立直角坐标系 $Oxyz$ ，在 $yOz$ 平面处放置一个厚度为 $t$ 的凸透镜，凸透镜的中心位于 $O$ 点，两个折射面的曲率半径的绝对值均为 $R$ ，制作凸透镜的材料的折射率为 $n_0$ . 如果 $xOy$ 平面内有一个物体，该物体的外形轮廓可由方程 $\left(x-x_0\right)^2+y^2=a^2$ 表示, 其中 $x_0 < -\frac{t}{2}, 0 < a < -\frac{t}{2}-x_0$ ， 在傍轴近似下求该物体经透镜所成的像的轮廓方程. (15分)
   7. 将 $N$ 个厚度为 $t$ 的凸透镜紧贴在一起构成一个光学系统，所有透镜的主光轴重合，每个折射面均为曲率半径的绝对值为 $R$ 的部分球面，制作透镜的材料的折射率为 $n_0$ . 在傍轴近似下，如果空间中一点有一条折射参数和位置参数分别为 $r_1$ 、 $d_1$ 的光线，该点经该光学系统所成的像点处的对应光线的折射参数和位置参数分别为 $r_2$ 、 $d_2$ ，定义：\[\Phi=\frac{r_2}{d_1}-\frac{r_1}{d_2}\]叫做该光学系统的光焦度，请计算该光学系统的光焦度，用仅含 $t$ 、 $R$ 、 $n_0$ 、 $N$ 这些与光学系统本身的性质有关的量的表达式表示，并简单解释光焦度的物理意义. (16分)
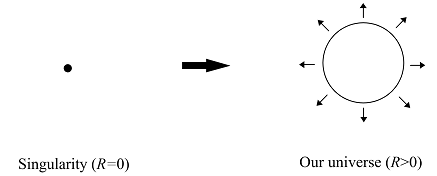
2. 关于宇宙的起源，现在最广为接受的是宇宙大爆炸. 该理论认为宇宙起源于一个密度与温度极高的奇点， 并不断膨胀成为今天的宇宙. 然而关于宇宙的体积是有限还是无限、宇宙的形状等问题至今尚无定论，为具体起见，我们假设宇宙是一个三维球面 $S^3$ . 三维球面是四维空间中四维球体的表面，若它的半径为 $R$ ，则它的体积等于 $V=2\pi^2R^3$ . 宇宙膨胀的过程， 就相当于宇宙的半径 $R(t)$ 从0开始随时间逐渐增长的过程，如图所示. 在宇宙诞生的早期，温度极高，粒子的动能极大，它们的质量 均可以忽略，因此可认为此时宇宙中充满了静止质量为0的“辐射气体”，这段时期称为由辐射主导的宇宙. 对于辐射气体，它的压强 $p$ 、温度 $T$ 和内能密度 $u$（包含静止能量）的关系满足 $p=u/3,\quad u=kT^4$. 其中 $k$ 是已知常数. 当宇宙继续膨胀，辐射气 体逐渐冷却，直到内能远小于静止能量时，宇宙进入由物质主导的阶段，此时的物质压强和内能密度满足 $p \ll u$. 假设已知宇宙温度为 $T_c$ 时由辐射主导转换为物质主导，此时的宇宙半径为 $R_c$，为简单起见，假设所有的辐射气体在此时全部转化为动能远小于静 止能量的物质. 本题中假设宇宙是均匀的，即任何物理量仅依赖于时间，与位置无关. 引力常数为 $G$ ，真空光速取 $c=1$ .
   
   1. 写出能量守恒定律的内容. (2分)
   2. 在辐射主导阶段与物质主导阶段，宇宙中的总内能分别是否守恒？试解释守恒或不守恒的原因. (6分)
   3. 如果宇宙膨胀可以视为宇宙中的辐射气体或物质在做绝热膨胀，试分别推导辐射主导阶段的宇宙和物质主导阶段的宇宙中的内能密度与宇宙半径的关系式 $u(R)$ .(10分)
   4. 为了求解宇宙半径如何随时间演化 $R(t)$ ，我们在某时刻的宇宙空间中划分出一个球体区域，这个球体之于宇宙这个三维球面就好比一个二维球面上的圆斑之于该二维球面. 当二维球面膨胀时，圆斑也会变大，同理，由于宇宙的膨胀，宇宙中任一球体区域也会逐渐变大. 假设有一观测者处于该球体区域中心，他将会看到球体表面上的一个粒子由于宇宙膨胀而离他远去，但从牛顿力学的观点，球体表面的粒子在该球体区域的万有引力下运动. 试以该观测者的角度对粒子使用牛顿第二定律或机械能守恒定律，证明宇宙半径 $R(t)$ 的演化满足：\[\left(\frac{\dot{R}}{R}\right)^2+\frac{C}{R^2}=\frac{8 \pi G}{3} u\]其中 $\dot{R}$ 表示 $R$ 对时间的导数， $u$ 为宇宙中的内能密度， $C$是一常数. (10分)
   5. 在(4)的条件下，对于我们感兴趣的三维球面宇宙，通常取 $C=1$ . 宇宙在由辐射主导转换为由物质主导后，宇宙会膨胀到一个最大体积，之后宇宙会开始收缩，直到收缩回一个奇点. 试求宇宙能够达到的最大体积 $V_m$ .(12分)
   6. 在(4)的条件下，取 $C=1$ . 试推导在辐射主导阶段的宇宙半径 $R(t)$ 、宇宙内能密度 $u(t)$ 的表达式，并求解宇宙由辐射主导阶段转为物质主导阶段的时刻 $t_c$ .(17分)
   7. 物理学家发现，我们的世界很可能存在“宇宙学常数”. 这意味着，即便在空无一物的真空，也可能存在引力效应，换句话说，真空可能本身具有能量，这即是“真空能”. 真空能的绝对大小在宇宙学中切实可测. 因此，等价于引入“宇宙学常数”，我们可以假定真空具有能量密度 $u_v$ ，并且真空会贡献具有和这个能量密度相反的负压强 $p_v=-u_v$ . 实际上，在宇 宙早期，当辐射主导的宇宙冷却到辐射气体的内能密度小于真空能量密度时，宇宙会由于真空能的主导作用而经历一个“暴胀”阶段，这就是暴胀宇宙. 暴胀宇宙可以解释前六问讨论的仅有两个阶段的标准宇宙不能解释的问题. 若已知宇宙暴胀开始时的宇宙半径为 $R_e$ ，试求暴胀开始时宇宙的大致温度 $T_e$，以及宇宙暴胀过程中的 $R(t)$ 表达式，为简单起见设 $u_v$ 恒定且已知，并假设宇 宙暴胀开始前宇宙能量由辐射主导，而暴胀开始后辐射气体能量可以忽略（该问可以假设 $\dot{R}\ll 1$ ）. (18分)
3. 本题考虑软绳与弹簧的问题.

   · 一条软绳摆在水平桌面上，整条绳子的原长为 $L$，质量为 $m$ ，与桌面摩擦系数为 $\mu$ ，在绳 子的一端沿着绳子的方向施加拉力向外拉动绳子，拉力从0开始缓慢增大. 重力加速度为 $g$ .

   1. 写出牛顿第二定律与牛顿第三定律的内容. (3分)
   2. 若绳子可伸长，且整条绳子的劲度系数为 $k$ ，将绳子在桌面上摆成一条直线，试求当绳子两端均 自由，即不给绳子施加拉力的情况下，绳子在桌面上能够保持静止的最大可能长度. (7分)
   3. 若绳子可伸长，且整条绳子的劲度系数为 $k$ ，将绳子在桌面上摆成一条直线，现在绳子一端施加 从0开始缓慢增大的拉力，当绳子未施加拉力的一端刚刚开始移动时，试求此时拉力 $F$ 的大小以及绳子的长度. (8分)
   4. 在(3)的条件下，试求绳子未施加拉力的一端开始移动前，在绳子被拉一端的拉力与绳长的关系式 $s(F)$ .(11分)
   5. 若绳子不可伸长，将绳子摆成圆心角为 $\alpha$ 的圆弧形状，在绳子一端施加从0开始缓慢增大的 沿绳方向的拉力，当绳子刚刚被拉动时，试求此时拉力 $F$ 的大小. (11分)
   6. 在(5)的条件下，将绳子首尾相接，使其成为一条周长为 $L$ 的圆形绳子. 现使绳子脱离桌面，并令圆形绳绕其圆心以恒定的角速度 $\omega$ 转动. 假设某时刻圆形绳在某处突然断裂，不妨设断裂点处于 $\theta=0$ ，不计圆形绳的重力，试求圆形绳断裂后瞬间绳上各点的加速度 $a(\theta)$ 的表达式. (12分)

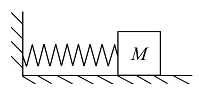
   · 一段自然放置时质量线密度为 $\lambda$，原长为 $L$ ，整体劲度系数为 $k$ 的弹簧. 将弹簧的一端固定于墙壁，另外一端连接一个光滑桌面上的质量为 $M$ 的物体，如图所示. 假设弹簧与物体在弹簧弹性限度内做微小振动.
   

   7. 如果近似认为弹簧在振动过程中是均匀伸长的，试求系统的振动频率. (6分)
   8. 试求该系统振动的本征频率. 并分析在何种极限下会回到(7)中的结果. (17分)
4. 本题将对一个有趣的断言展开分析：一个理想的光滑的对称球体，在经典力学（牛顿引力）框架下将无法使用宏观力学手段区分它是静止的还是绕其一条直径转动. 这是由于其对称性，任何接触形式的相互作用都难以展示出其两种运动状态之间的区别：光滑导致没有摩擦，对称导致无法从视觉上进行判断（当然这来自经典的几何光学断言）.
   1. 试简要阐释电场与磁场的关系. (2分)
   2. 考虑一个足够简单的情形，一个理想光滑长方体，其长是无穷的，且沿着 $Ox$ 轴放置，相应地宽沿着 $Oy$ 轴，为 $w$，高则沿着 $Oz$ 轴，为 $h$. 设法令其携带均匀分布的电荷，电荷体密度为 $\rho$. 试计算长方体外足够远处的 电场分布. (5分)
   3. 在(2)的条件下，试计算长方体外足够远处的磁场分布，你会发现这是一个用于检查长方体是沿着 $Ox$ 轴做匀速直线运动还是静止的一个可行方案. (6分)
   4. 对于(2)与(3)的问题，尝试设计一个不同的实验方案来检验它是否在沿着 $Ox$ 轴做匀速运动，假定引力规律遵循牛顿引力. (6分)

   · 以下假设物体由可以在物体中自由移动的电量为 $e$，质量为 $m$ 的微观粒子，以及同这些粒子电性相反，彼此相对静止的均匀背景共同组成，并同时保证物体整体呈电中性. 假设构成物质的带电粒子间仅存在电磁相互作用.

   5. 如果长方体沿 $Ox$ 轴做匀加速直线运动，则稳恒运动时（即电荷相对物体静止），前面所提出的长方体将均匀带电的假设不再成立. 证明此时电荷仅分布在长方体的表面. (8分)
   6. 考虑一个理想的光滑的圆柱体，其高足够大，半径为 $R$ . 若其绕轴线以角速度 $\omega$ 做稳恒 的转动，圆柱体是电中性的，即其单位长度的电荷量为 $0$ ，试分析其内部的电荷分布. (14分)
   7. 在(6)的条件下，试求圆柱体内部与外部的电磁场分布，并分析这是否可以用来判断圆柱是静止的还 是转动的. (14分)
   8. 考虑一个半径为 $R$ 的光滑球体，试分析(6)与(7)中的方案能否用来判断该光滑球体是否在旋转. (20分)

第十届OPhO决赛参考答案

1. 1. 当物体发出的光经光学元件后能会聚为一点时，像是清晰的，不能会聚为一点时，像是模糊的，这就是决定像清晰与否的条件. 能成真正清晰的像的光学元件很少，如平面镜. （言之有理即可）
   2. 折射定律为：\[n_1 \sin \theta_1=n_2 \sin \theta_2 \]傍轴条件下的折射定律为： \[n_1 \theta_1=n_2 \theta_2 \]
   3. \[r_2=r_1+\frac{n_2-n_1}{R} d_1, \quad d_2=d_1 \]
   4. \[r_2=r_1 \qquad d_2=-\frac{l}{n} r_1+d_1 \]
   5. 证明略.
   6. \[\begin{aligned}&\frac{\left(x^{\prime}-\frac{t}{2}-\frac{-\frac{t}{n_0}+\left(-\frac{t}{2}-x_0\right)\left(1-\frac{n_0-1}{n_0} \frac{t}{R}\right)}{1-\frac{n_0-1}{n_0} \frac{t}{R}+\left(-\frac{t}{2}-x_0\right)\left(\frac{2\left(n_0-1\right)}{R}-\frac{t}{n_0}\left(\frac{n_0-1}{R}\right)^2\right)}\right)^2}{\left(\frac{-\frac{t}{n_0}+\left(-\frac{t}{2}-x_0\right)\left(1-\frac{n_0-1}{n_0} \frac{t}{R}\right)}{1-\frac{n_0-1}{n_0} \frac{t}{R}+\left(-\frac{t}{2}-x_0\right)\left(\frac{2\left(n_0-1\right)}{R}-\frac{t}{n_0}\left(\frac{n_0-1}{R}\right)^2\right)}-\frac{-\frac{t}{n_0}+\left(\frac{t}{2}-x_0-a\right)\left(1-\frac{n_0-1}{n_0} \frac{t}{R}\right)}{1-\frac{n_0-1}{n_0} \frac{t}{R}+\left(-\frac{t}{2}-x_0-a\right)\left(\frac{2\left(n_0-1\right)}{R}-\frac{t}{n_0}\left(\frac{n_0-1}{R}\right)^2\right)}\right)^2}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad+\frac{y^{\prime 2}}{\left(\frac{a}{1-\frac{n_0-1}{n_0} \frac{t}{R}+\left(-\frac{t}{2}-x_0\right)\left(\frac{2\left(n_0-1\right)}{R}-\frac{t}{n_0}\left(\frac{n_0-1}{R}\right)^2\right)}\right)^2}=1\end{aligned}\]
   7. 光焦度是： \[A_{11}\left(S^{\prime}\right)_{11}^N\left(A^{-1}\right)_{12}+A_{12}\left(S^{\prime}\right)_{22}^N\left(A^{-1}\right)_{22}\] 其中 $S^\prime$ 是对角矩阵： \[ S^{\prime}=A^{-1} S A\] 而：\[S=\left(\begin{array}{cc} 1-\frac{n_0-1}{n_0} \frac{t}{R} & \frac{2\left(n_0-1\right)}{R}-\frac{t}{n_0}\left(\frac{n_0-1}{R}\right)^2 \\-\frac{t}{n_0} & 1-\frac{n_0-1}{n_0} \frac{t}{R}\end{array}\right) .\] 光焦度反映了光学系统对光线的偏折情况，光焦度大于 0 表示光学系统对光线起会聚作用，光焦度小于 0 表示光学系统对光线起发散作用，光焦度的绝对值越大光学系统对光线的偏折能力越强.
2. 1. 在孤立系统中，能量既不会凭空产生，也不会凭空消失，它只会从一种形式转化为另一种形式，或者从一个物体转移到其它物体，这个过程中能量的总和保持不变.
   2. 辐射主导阶段不守恒；物质主导阶段守恒. 原因是如果将宇宙膨胀视为宇宙中气体的绝热膨胀，则在辐射主导阶段由于宇宙体积增大，辐射气体的膨胀会做功，从而内能不守恒，相当于是说宇宙中辐射气体本身并不是孤立系统，本质上，这是因为宇宙 本身是一个变化的弯曲时空，辐射气体与弯曲时空存在耦合，宇宙弯曲蕴含的引力能与辐射气体的总体才是孤立系统. 对于物质主导阶段，物质的压强本身可以忽略，故不会在绝热膨胀过程中做功，故内能守恒.
   3. 辐射主导阶段： \[u=kT_c^4\left(\frac{R}{R_c}\right)^{-4}\] 物质主导阶段： \[u=kT_c^4\left(\frac{R}{R_c}\right)^{-3}\]
   4. 证明略.
   5. \[V_m=\frac{1024}{27}\pi^5 G^3k^3R_c^9T_c^{12}\]
   6. \[R(t)=\sqrt{R_c^2T_c^2\sqrt{\frac{32 \pi Gk}{3}}t-t^2}\]\[u(t)=kT_c^4R_c^4\left(T_c^2R_c^2\sqrt{\frac{32 \pi Gk}{3}}t-t^2\right)^{-2}\]\[t_c={T_c^2R_c^2\sqrt{\frac{8 \pi Gk}{3}}-R_c\sqrt{\frac{8 \pi GkT_c^4R_c^2}{3}-1}}\]
   7. \[T_e=\left(\frac{u_v}{k}\right)^{\frac{1}{4}}\]\[R(t)=R_e\mathrm{e}^{\sqrt{A}(t-t_e)}\]其中：\[A=\frac{8 \pi G}{3} u_v \]\[t_e={R_e^2\sqrt{\frac{8 \pi Gu_v}{3}}-R_e\sqrt{\frac{8 \pi Gu_vR_e^2}{3}-1}}\]
3. 1. 牛顿第二定律：物体加速度的大小跟作用力成正比，跟物体的质量成反比，且与物体质量的倒数成正比；加速度的方向跟作用力的方向相同. 公式：$\vec{F}=m\vec{a}$ . 牛顿第三定律：相互作用的两个物体之间的作用力和反作用力总是大小相等，方向相反，作用在同一条直线上.
   2. \[s_m=L+\frac{\mu mg}{4k}\]
   3. \[s=L+\frac{\mu mg}{2k}\]\[F={\mu mg}\]
   4. \[s=L+\frac{F^2}{2\mu k mg}\]
   5. \[F= \begin{cases}\frac{\mu m g}{\alpha} \sin \alpha & \left(0 < \alpha \leq \frac{\pi}{2}\right) \\ \frac{\mu m g}{\alpha} & \left(\frac{\pi}{2} < \alpha < 2 \pi\right)\end{cases}\]
   6. \[a_\theta=-\omega^2 \frac{L}{2\pi} \frac{\sinh (\theta-\pi)}{\cosh \pi}\]
   7. \[\omega=\sqrt{\frac{k}{M}}\]
   8. \[ \tan\left(\omega \sqrt{\frac{\lambda L}{k}}\right)=\frac{\sqrt{\lambda Lk}}{M\omega}\]当 $M\gg \lambda L$，时：\[\omega=\sqrt{\frac{k}{M}}\] 回到了(7)的结果，这是频率最小的一支解的关于参数$\lambda L/M$的一阶近似解.
4. 1. 变化的电场能够产生磁场，变化的磁场能够产生电场. 纯电场在不同的惯性参考系下可能表现为磁场，反之亦然. 这说明电场与磁场是同一物理本质（电磁场）的两种不同表现形式，它们是深刻统一的，电磁对偶对称性亦能体现这一点. （言之有理即 可）
   2. \[E=\frac{\rho w h}{2 \pi \epsilon_0 r} \]方向垂直于直线向外. 其中 $r$ 为场点到 $O x$ 轴的距离.
   3. \[B=\frac{\mu_0 \rho w h v}{2 \pi r} \]方向按照右手螺旋规则判断. 如果长方体运动速度 $v$ 不为零，则存在非零磁场，从而可以检查长方体是否做匀速直线运动.
   4. 例如，可以在空间中施加沿 $O y$ 方向的均匀磁场 $B$, 检查 $O z$ 方向的电势差的变化（霍尔效应）等.
   5. 证明略.
   6. 体电荷密度： \[n(r)-\frac{2 m c^2}{\mu_0 e} \frac{\omega^2}{\left(c^2-\omega^2 r^2\right)^2}\]表面电荷密度：\[\sigma=\frac{\epsilon_0 m c^2}{e R} \frac{\omega^2 R^2}{c^2-\omega^2 R^2} .\]
   7. \[\begin{aligned}& E(r)=-\frac{m c^2 r}{e R^2} \frac{\omega^2 R^2}{c^2-\omega^2 r^2} \\& B(r)=\frac{m \omega}{e} \frac{\omega^2 r^2}{c^2-\omega^2 r^2}\end{aligned}\]在无穷长的情形下，圆柱体外部不存在电场或磁场. 因此这种方法并不足以用于判断圆柱体是否在转动. 但由于圆柱体自身携带有表面电荷，因此分析其表面和轴线之间的电势差同样能够判断圆柱体的转动情况.
   8. 电中性条件：\[\sigma 4 \pi R^2+n \frac{4}{3} \pi R^3=0 \]转动球体的总磁矩的零头阶：\[m =2 \pi n \omega \frac{R^5}{5}+2 \sigma \omega R^2\neq 0\]故可以根据球外是否有电磁场分布来确定球是否是转动的.